Uitleg artikel algemene relativiteitstheorie: paragraaf 4
Trefwoorden: algemene relativiteitstheorie, Annalen der Physik, Die Grundlage der allgemeinen Relativitätstheorie/De grondslag van de algemene relativiteitstheorie, Königlich Preussischen Akademie der Wissenschaften/Koninklijke Pruisische Academie der Wetenschappen
Hoofdstuk A:
Principiële overwegingen bij het relativiteitsbeginsel.
Paragraaf 4:
De relatie tussen de vier coördinaten die we verkrijgen uit ruimte- en tijdmeetresultaten.
Een analytische uitdrukking voor het zwaartekrachtveld.
Deze paragraaf is de laatste paragraaf van hoofdstuk A.
Einstein neemt wederom het woord om iets te zeggen in zijn algemeenheid over de wereld om ons heen.
Het streven van de natuurkunde is om met een minimaal aantal wetten, zo ‘zuinig’ mogelijk, de wereld om ons heen te beschrijven.
Je kunt een natuurkundewet formuleren waarmee je kunt rekenen aan je fietstocht om morgen op school of op je werk te komen, en je
kunt een natuurkundewet formuleren die de autorit beschrijft hoe je in het weekend bij je oma komt.
Maar beter is het om een wet te formuleren die beweging in het algemeen beschrijft.
Bijvoorbeeld de volgende wet: s = vt.
Hier staat dat de afgelegde weg (s, van spatium, dit is Latijn voor ruimte) gelijk is aan de snelheid (v, van velocity, dit is
Engels voor snelheid) maal de verstreken tijd (t, van tijd).
Als je een half uur fietst met een snelheid van 15 km/uur, dan is de afgelegde weg naar school of werk 0.5 × 15 = 7.5 kilometer.
En als de autorit naar oma drie kwartier (= 0.75 uur) duurt bij een gemiddelde snelheid van 80 km/uur, dan is de afgelegde weg
0.75 × 80 = 60 kilometer.
Met één natuurkundewet kunnen we aan beide bewegingen rekenen.
Een ander voorbeeld is een wet van Newton: F = ma.
Hier staat dat de kracht (F, van force, dit is Engels voor kracht) die op een lichaam wordt uitgeoefend gelijk is aan de
massa (m, van massa) van dat lichaam maal de versnelling (a, van acceleration, dit is Engels voor versnelling) die dat lichaam
ondergaat.
En of die kracht een zwaartekracht of een elektrische kracht of wat dan ook voor kracht is, dat maakt niet uit.
Maar Einstein zegt dat het helemaal niet zijn hoofddoel is om zo zuinig mogelijk de algemene relativiteitstheorie voor het
voetlicht te brengen, het gaat hem er helemaal niet om dat het zo eenvoudig mogelijk is, en dat het zo logisch mogelijk is,
en dat er gebruik gemaakt wordt van een minimum aan axioma’s (axioma’s zijn onbewezen aannames, de basale uitgangspunten,
zoals bijvoorbeeld één plus één is twee).
Hij wil vooral dat de lezer meegaat in Einstein’s overtuiging dat dit de meest logische weg is om te gaan, oftewel ‘dat dit
psychologisch de meest natuurlijke weg is’ (jawel, geloof het of niet maar er is hier een natuurkundige aan het woord).
Verder wil hij dat de vóóronderstellingen die hij maakt in overeenstemming zijn met onze dagelijkse ervaringen.
Hierop voortbordurend lanceert Einstein de vooronderstelling: in oneindig kleine vierdimensionale gebieden kan de beperkte
relativiteitstheorie toegepast worden, indien het coördinatensysteem maar goed gekozen wordt.
Met vierdimensionaal bedoelt Einstein lengte, breedte en hoogte, de drie ruimtelijke dimensies, en de tijd als vierde dimensie.
En de “beperkte relativiteitstheorie” is wat tegenwoordig te boek staat als de “speciale relativiteitstheorie”.
Maar wat is nou precies ‘oneindig klein’?
En wat is een ‘goed coördinatensysteem’?
Stel, X1, X2 en X3 kiezen we als de ruimtelijke coördinaten lengte, breedte en hoogte.
En X4 is de tijdcoördinaat.
In de voetnoot merkt Einstein nog op dat de lichtsnelheid-in-vacuüm zo gekozen wordt dat die gelijk aan één is.
Dit “-in-vacuüm” hoort er wel bij, want licht dat door lucht of glas heen gaat heeft een andere snelheid (het is langzamer)
dan licht dat voortraast in vacuüm.
Dat is gewoon een kwestie van je basiseenheden ‘effe’ herdefiniëren, dat maakt je vergelijkingen een heel stuk overzichtelijker want
je hoeft dan niet overal die c voor de lichtsnelheid mee te slepen.
Ergens aan het eind plakken we die er wel weer in.
Hiervoor had ik het over de wet: s = vt.
Of het dan gaat over meters of kilometers of yards is van later zorg.
Indien ik een ruimtelijke afstand wil uitrekenen dan gebruik ik de
stelling van Pythagoras:
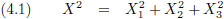
Nu gaan we een stapje verder door de tijdcoördinaat erbij te betrekken, en we hebben het nu dus niet meer over
een
ruimtelijke afstand, maar over een afstand in de
ruimtetijd.
Dat ziet er dan als volgt uit:
En nu gebeurt er ineens heel veel.
De kleine letter s geeft een afstand aan in de ruimtetijd.
Einstein heeft het over een “
lijnelement”, maar wat heel vaak wordt gebruikt in de literatuur is de
term “
interval”.
Wij gaan hier
niet met Einstein mee en praten over interval.
Ik maak vergelijking (4.2) iets overzichtelijker door de ruimtecoördinaten samen te nemen als volgt:
En dit wil ik graag vergelijken met een
ruimtelijke afstand in
twee dimensies:
Stel dat twee voorwerpen, bijvoorbeeld jij en ik, een constante
ruimtelijke afstand tot elkaar houden.
In vergelijking (4.4) betekent dat dat X = constant, bijvoorbeeld 3 meter.
Wanneer ik alle punten in een grafiek zet waarbij mijn afstand constant is ten opzichte van jou dan ziet dat er zo uit:
Figuur 4.1
Inderdaad, dat is een cirkel.
Als ik ten opzichte van jou kan bewegen, maar ik zit met een metalen stang aan jou vast zodat onze onderlinge afstand gelijk
blijft, dan kan ik niet anders dan een cirkel om jou heen beschrijven (of jij een cirkel om mij heen).
Want als ik in vergelijking (4.4) de afstand X vervang door een constante p (ik wil de letter c vermijden, omdat die staat voor de
lichtsnelheid en mogelijk verwarring op kan roepen) en de vergelijking nog wat herschik, dan staat er:
En dit is inderdaad de vergelijking van een cirkel.
Maar hoe ziet het er dan uit wanneer ik in de
ruimtetijd beweeg op een constant
interval (ruimtetijdafstand) van jou?
Laten we in vergelijking (4.3) s dan maar vervangen door de constante p en de vergelijking nog wat herschikken als volgt:
Wat natuurlijk direct opvalt is dat in vergelijking (4.5) een minteken staat en in vergelijking (4.6) een plusteken.
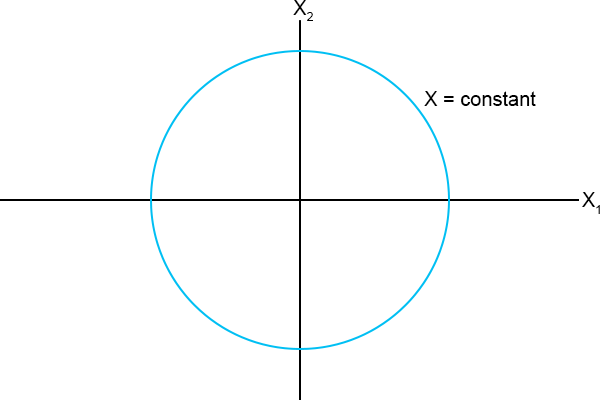
Laten we van vergelijking (4.6) ook maar eens een grafiek maken.
Figuur 4.2
Een relatief eenvoudig plaatje, maar hier is heel veel over te vertellen.
Eerst even ere wie ere toekomt: het was Hermann Minkowski die in 1907 de speciale relativiteitstheorie omschreef naar een elegant wiskundig bouwwerk.
Vergelijking (4.2), hoe simpel die er ook uitziet, is gebaseerd op zijn werk.
Wat zien we in figuur 4.2?
De hyperbolen zijn lijnen die een constant interval beschrijven, vergelijkbaar met de cirkel in figuur 4.1 die een constante
ruimtelijke afstand beschrijft.
Daarnaast is er de oorsprong, daar zijn X = 0 en X4 = 0, oftewel wij bevinden ons daar op dezelfde plaats en dezelfde
tijd in de ruimtetijd: we staan tegen elkaar aan.
Kijken we naar de verticale as, dat is de verzameling punten waar de ruimtelijke afstand X = 0, dan bevinden zich daar twee snijpunten
met de kromme: X4 = +p en X4 = −p.
Op die twee punten bevind ik mij op dezelfde plaats in de ruimte, maar op een andere tijd.
Ik ben dan op dezelfde ruimtelijke positie als jij, maar eerder (onderste snijpunt met de verticale as) of later (bovenste snijpunt met de verticale as).
Deze grafiek geeft dan ook aan hoe wij ons tijdachtig ten opzichte van elkaar bevinden.
De twee stippellijnen, die ik onder een hoek van 45 graden met de assen erbij getekend heb, zijn de asymptoten van de grafiek.
Asymptoten zijn lijnen waar een kromme naartoe nadert wanneer een bepaalde variable naar oneindig (∞) gaat.
Dus stel dat X = ∞, dan is p te verwaarlozen en staat er X4 = +X of X4 = −X.
En dit zijn inderdaad vergelijkingen van lijnen die een hoek van 45 graden maken met de assen.
Hiervoor heb ik verteld dat we de lichtsnelheid c voor het gemak uit de vergelijkingen laten, maar eigenlijk staat er voor
X4: X4 = ct.
Daarmee is de vergelijking van de asymptoot: X = ct, oftewel wanneer je je verplaatst met de lichtsnelheid.
De asymptoot is een lijn die je kunt benaderen, maar de kromme zal nooit samenvallen met de asymptoot, want dat zou betekenen dat er gereisd
wordt met de lichtsnelheid en dat kan niet.
In vergelijking (4.2) zijn de ruimtecoördinaten met een minteken aangegeven en de tijdcoördinaat met een plusteken.
Waarom eigenlijk?
Zullen we voor de grap mintekens en plustekens eens omwisselen?
Vergelijking (4.2) wordt dan:
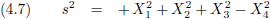
En vergelijking (4.6) wordt dan:
Deze kromme willen we natuurlijk ook even zien in een plaatje.
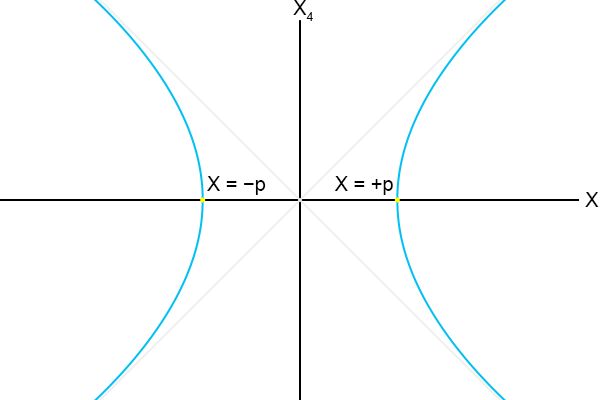
Figuur 4.3
De figuur hierboven is een gekantelde versie van figuur 4.2.
Wat stellen nu de snijpunten met de assen voor?
Het rechtersnijpunt met de horizontale as betekent dat wij ons p meters van elkaar verwijderd bevinden, maar wel op hetzelfde tijdstip.
En voor het linkersnijpunt met de horizontale as geldt hetzelfde, maar bij het ene snijpunt bevindt de een zich voor de ander,
en bij het andere snijpunt erachter.
Of het is een verschil van onder en boven, of links en rechts.
Deze grafiek geeft dan ook aan hoe wij ons
ruimteachtig ten opzichte van elkaar bevinden.
En de asymptoten geven weer aan dat de een zich met de lichtsnelheid verwijdert van de ander, een onhaalbare situatie.
Dan is het natuurlijk ook leuk om de beide plaatjes, figuur 4.2 en figuur 4.3, te combineren.
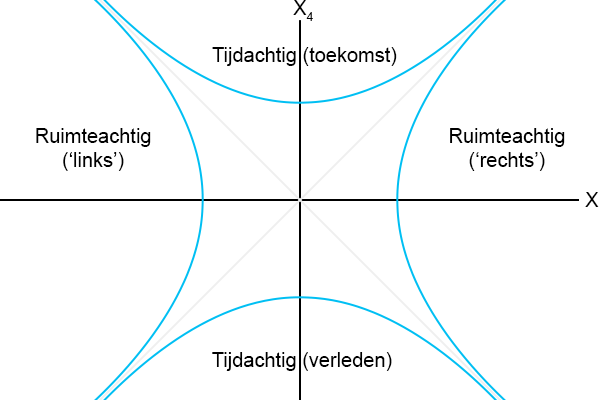
Figuur 4.4
Stel dat jij je in de oorsprong van het assenstelsel bevindt en ik ben ergens in het bovenste kwadrant “Tijdachtig (toekomst)”,
dan zijn wij altijd ‘door de tijd gescheiden’.
Ik kan wel zijn waar jij bent, maar
nooit op hetzelfde moment, ik ben altijd in jouw toekomst.
Tenzij s = 0 natuurlijk, dan zijn we gezellig samen in de oorsprong.
En ben ik in het onderste kwadrant “Tijdachtig (verleden)” dan zijn wij ook altijd ‘door de tijd gescheiden’.
Wederom kan ik wel zijn waar jij bent, maar
nooit op hetzelfde moment, altijd ben ik in jouw verleden.
In het linkerkwadrant “Ruimteachtig (‘links’)” of het rechterkwadrant “Ruimteachtig (‘rechts’)” kan ik
nooit ruimtelijk zijn waar jij bent, altijd ben ik ‘links’ of ‘rechts’ van jou (of boven of onder, of voor of achter,
daarom staan links en rechts ook tussen quotes).
De vier hyperbolen hebben ieder een snijpunt met een horizontale of verticale as.
En afhankelijk van de constante p liggen die vier snijpunten dichter bij de oorsprong, indien p kleiner wordt, of ze liggen
juist verder weg van de oorsprong wanneer p groter wordt.
Afhankelijk van de waarde van p doorloopt een hyperbool dus het gehele kwadrant dat gelegen is tussen twee asymptoten.
Daarom maar gelijk door naar het volgende plaatje waar ik de hyperbolen helemaal weglaat, want afhankelijk van de waarde
van p ‘vullen’ ze immers het gehele kwadrant.
Ieder punt in de grafiek is een gebeurtenis, een
puntgebeurtenis, waar Einstein het al eerder over had
(in
paragraaf 3).
En de grafiek geeft aan wat de onderlinge relatie is tussen die puntgebeurtenissen, liggen ze in elkaars verleden of toekomst,
of zijn ze ruimteachtig gescheiden en daarmee
niet in elkaars verleden of toekomst.
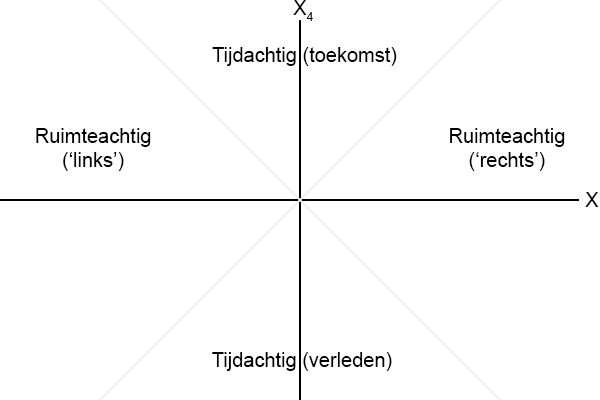
Figuur 4.5
Dit is weliswaar een tweedimensionaal plaatje, hij is gewoon vlak, maar we moeten niet vergeten dat de horizontale as
de totale drie-dimensionale ruimte uitbeeldt.
Probeer dat maar niet voor ogen te krijgen, want dat lukt toch niet, als je het maar wel in je achterhoofd houdt.
Vanuit de oorsprong gezien kun je de asymptoten dus zien als kegels van licht (
lichtkegels), het deel boven de
horizontale as is de toekomst (gezien vanuit de oorsprong!) en het deel beneden de horizontale as is het verleden
(gezien vanuit de oorsprong!).
Alles wat buiten die twee kegels ligt is ruimteachtig van jou gescheiden en is voor jou
verleden noch toekomst.
En datgene wat precies op de kegels gebeurt, dus op de asymptoten, reist met de snelheid van het licht en dat noemen we
lichtachtig.
Samengevat wordt dit:
- Een deeltje (iets stoffelijks dus, iets dat altijd langzamer is dan het licht) dat de oorsprong verlaat
kan alleen datgene beïnvloeden wat binnen de toekomst-kegel ligt.
s2 > 0 oftewel s > 0 (het interval s is positief).
- Een lichtstraal (die gaat uiteraard met de snelheid van het licht) die de oorsprong verlaat
kan alleen datgene beïnvloeden wat op de toekomst-kegel ligt.
s2 = 0 oftewel s = 0 (het interval s is nul).
- Een deeltje (iets stoffelijks dus, iets dat altijd langzamer is dan het licht) kan alleen datgene
beïnvloeden wat in de oorsprong gebeurt indien het binnen de verleden-kegel ligt.
s2 > 0 oftewel s > 0 (het interval s is positief).
- Een lichtstraal (die gaat uiteraard met de snelheid van het licht) kan alleen datgene
beïnvloeden wat in de oorsprong gebeurt indien het op de verleden-kegel ligt.
s2 = 0 oftewel s = 0 (het interval s is nul).
- Er is niets wat in de oorsprong kan plaatsvinden dat ook maar enige invloed kan uitoefenen op
iets dat buiten de beide kegels gebeurt.
s2 < 0 oftewel s = imaginair (het interval s is niet reëel).
- Er is niets wat buiten de beide kegels kan plaatsvinden dat ook maar enige invloed kan
uitoefenen op iets dat in de oorsprong gebeurt.
s2 < 0 oftewel s = imaginair (het interval s is niet reëel).
Laten we onze waarnemers Jan en Piet er weer eens bij roepen.
We zetten Jan en Piet met de ruggen tegen elkaar aan, en maken daar op een bepaald moment van bovenaf een foto van.
Een foto legt in feite een gebeurtenis vast, vergelijkbaar met de puntgebeurtenissen waar Einstein het al eerder over had.
Het tijdstip dat de foto gemaakt wordt noemen we het tijdstip t.
Schematisch ziet dat er dan als volgt uit:

Figuur 4.6
Vervolgens begint Piet met constante snelheid te bewegen, hij begint te wandelen of scheurt weg met een raceauto of hij stapt
in een raket.
Het maakt niet uit hoe, het gaat erom dat hij zich met constante snelheid van Jan verwijdert.
En daar maken we ook telkens foto’s van, na vaste tijdsintervallen ∆t maken we telkens een foto.
Dus de eerstvolgende foto is na ∆t vanaf het begintijdstip t, oftewel na t + ∆t.

Figuur 4.7
En na ∆t weer een foto.

Figuur 4.8
En zo gaat het maar door, ∆t later weer een foto.

Figuur 4.9
Je raadt het al, ∆t later volgt de volgende foto.
Figuur 4.10
Uiteindelijk hebben we een indrukwekkende hoeveelheid foto’s: we hebben een heleboel gebeurtenissen vastgelegd.
We leggen ze allemaal op volgorde op een stapel, de eerste foto (= oudste gebeurtenis) onderop en de laatste foto
(= meest recente gebeurtenis) bovenop.
Daarna kijken we van de zijkant tegen de stapel foto’s en gaan we onze fantasie gebruiken.
We doen net of het fotopapier doorzichtig is en daardoor zien we alleen de inkt die op de foto’s gedrukt is.
Als je fantasie je niet in de steek laat, dan krijg je dit plaatje voor ogen:
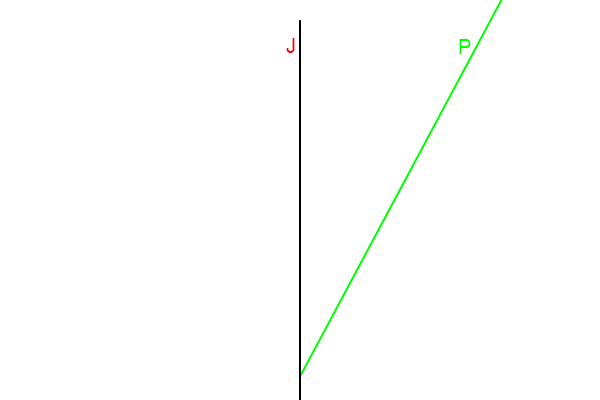
Figuur 4.11
Deze twee lijnen met de opeenvolgende gebeurtenissen laten de
wereldlijn van Jan en de
wereldlijn van Piet zien.
Alles volgt
wereldlijnen, van atomen tot vrachtwagens,
ze volgen allemaal
wereldlijnen.
En al deze
wereldlijnen vormen samen de
wereld.
Laat ik er maar eens een paar assen bijtekenen, dat geeft wat meer duidelijkheid.
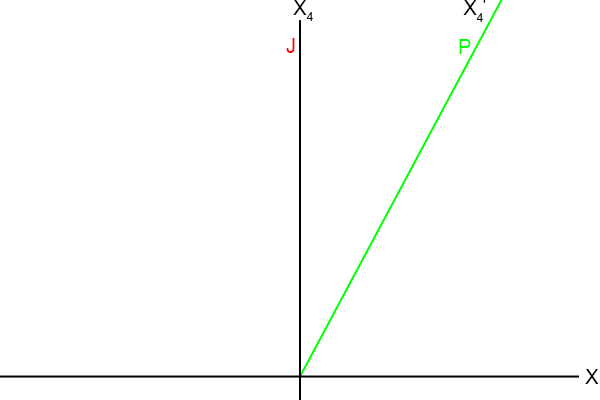
Figuur 4.12
Jan en Piet hebben allebei hun eigen X
4-as, hun eigen tijd-as, want twee bewegende stelsels, in dit geval Jan
en Piet, hebben allebei hun eigen tijdsbeleving zoals de speciale relativiteitstheorie al uitgebreid geleerd heeft.
Ze hebben dan wel ieder hun eigen tijd-as, maar
ruimtetijdintervallen zijn voor hen beiden gelijk.
Als Jan en Piet op drie
ruimtetijd meters afstand van elkaar
bewegen (een ruimtetijdinterval s van drie
meter), dan is dat zowel voor Jan als voor Piet als voor welke
bewegende waarnemer (met
constante snelheid)
dan ook drie meter.
Vergelijk het ermee als Jan en Piet bijvoorbeeld op drie
ruimtelijke meters afstand van elkaar
stilstaan
(een ruimte interval X van drie meter), dan is dat zowel voor Jan als voor Piet als voor welke
stilstaande waarnemer
dan ook drie meter.
Het ruimtetijdinterval s is dus
invariant, dat wil zeggen dat het ruimtetijdinterval s onafhankelijk is van de
waarnemer.
Drie meter ruimtetijd is voor Jan drie meter en ook voor Piet drie meter.
Vergelijk het met de ruimtelijke afstand X van vergelijking (4.4).
In figuur 4.2 is de kromme getekend met s, het ruimtetijdinterval, als constante p.
Laten we eens inzoomen op figuur 4.12 en de kromme van figuur 4.2, het constante ruimtetijdinterval, erbij intekenen.
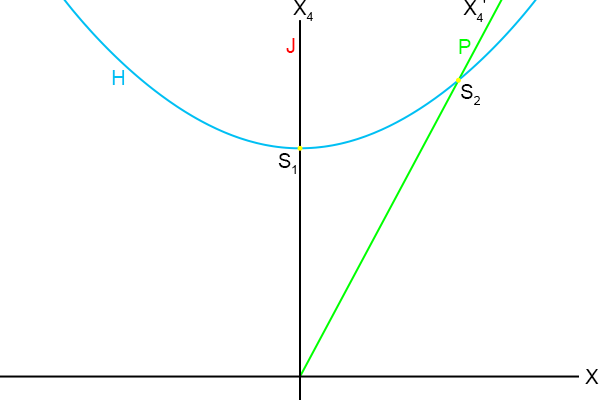
Figuur 4.13
Het is interessant om de snijpunten van de hyperbool met de
wereldlijnen van Jan en Piet nader te onderzoeken.
Laten we de vergelijkingen van de
wereldlijnen
en de hyperbool eens op een rijtje zetten.
Eerst de
wereldlijn
van Jan (Jan staat stil op de positie x = 0):
De
wereldlijn van Piet:
En dit is de hyperbool:
Waarbij geldt: β is de relatieve snelheid ten opzichte van de lichtsnelheid.
En kennen we de
Lorentz-factor γ al (of nog)?
Nu gaan we de beide snijpunten berekenen, eerst het snijpunt van de hyperbool met de
wereldlijn van Jan.
Dat is simpel, want de
wereldlijn van Jan zegt dat X = 0.
Dit vullen we in in de vergelijking van de hyperbool:
Het eerste snijpunt S
1 is dus (0, s).
Nu het tweede snijpunt, daarvoor stellen we de hyperbool gelijk aan de
wereldlijn van Piet:
En welke waarde van de
wereldlijn van Piet hoort daarbij?
Dan is het tweede snijpunt bekend: S
2 (sβγ, sγ).
En de volgende stap is om in de snijpunten de raaklijnen aan de hyperbool te berekenen.
Die raaklijnen zal ik er eerst bij intekenen:
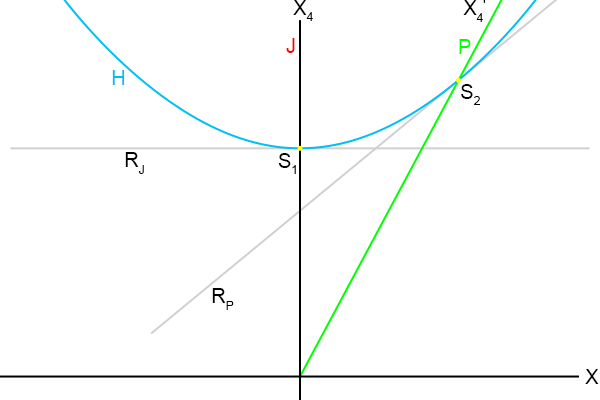
Figuur 4.14
Ik bepaal nu eerst de
afgeleide van de hyperbool.
Dit is de hyperbool:
En dit is zijn
afgeleide:
In deze vergelijking vullen we de X-waarden van de beide snijpunten in:
Daarmee hebben we de richtingscoëfficiënten (hellingsgetallen) van de raaklijnen, en die vullen we alvast in in de vergelijkingen
van de raaklijnen:
De beide b’s bepalen we door de respectievelijke snijpunten in te vullen.
En zo komen we tot de vergelijkingen van de raaklijnen:
En wat schieten we daar nu mee op?
Nou, als laatste stap gaan we de snijpunten berekenen van de beide raaklijnen met de
wereldlijn van ‘de ander’, en dan
wordt duidelijk waar ik heen wil.
Kijk maar in het volgende plaatje.
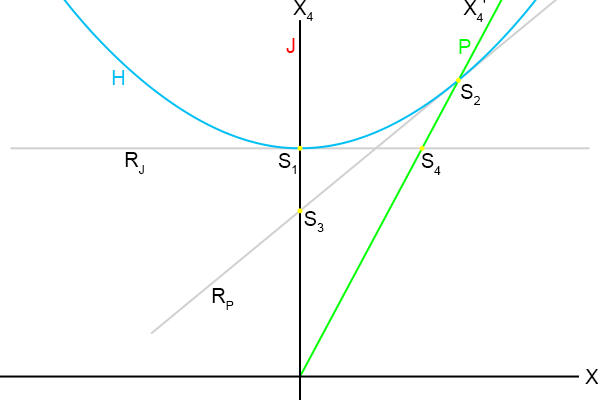
Figuur 4.15
Van de raaklijn R
p gaat het dus om het snijpunt S
3 met de
wereldlijn van Jan.
Die is simpel, want daar is X = 0 en dat vullen we in.
Dat levert op: R
p = s/γ, dus het snijpunt S
3 is (0, s/γ).
Voor het bepalen van het snijpunt van de raaklijn R
j met de
wereldlijn van Piet stellen we beide
vergelijkingen gelijk aan elkaar.
Als we dit invullen in de
wereldlijn
van Piet geeft dat: βs/β = s, dus snijpunt S
4 is (βs, s).
Tenslotte bepalen we van de snijpunten voor ieder de
ruimtetijd afstand tot de oorsprong.
Eerst voor S
3.
En daarna voor S
4.
Beide snijpunten hebben
hetzelfde ruimtetijdinterval tot de oorsprong!
Want wat gebeurt er?
Jan kijkt vanaf de gebeurtenis S
1 (alle punten van de grafiek zijn gebeurtenissen!) op zijn
wereldlijn (zijn tijd-as)
naar de
wereldlijn
van Piet (de tijd-as van Piet) via de raaklijn R
j.
Hij ziet de
wereldlijn van Piet op het
snijpunt S
4, de
gebeurtenis S
4.
Voor Jan is er inmiddels een ruimtetijdinterval s verstreken (alleen maar tijd, want Jan ‘beweegt niet’) vanaf de oorsprong en
hij ziet de klok bij Piet s/γ aanwijzen.
Vanuit Jan gezien loopt de klok van Piet langzamer:
tijddilatatie!
Piet daarentegen kijkt vanaf de gebeurtenis S
2 op zijn
wereldlijn (zijn tijd-as) naar de
wereldlijn van Jan (de tijd-as
van Jan) via de raaklijn R
p.
Hij ziet de
wereldlijn van Jan op het snijpunt
S
3, de
gebeurtenis S
3.
Voor Piet is er inmiddels een ruimtetijdinterval s verstreken (alleen maar tijd, want zijn
wereldlijn is zijn tijd-as en ook
Piet kan stellen dat hij ‘niet beweegt’) vanaf de oorsprong en hij ziet de klok bij Jan s/γ aanwijzen.
Vanuit Piet gezien loopt de klok van Jan langzamer: tijddilatatie!
Even samenvatten:
- De wereldlijn van Jan is zijn tijd-as,
hij kan daar continu NU roepen, want elk punt op die lijn is
voor hem NU (in de werkelijkheid bestaat er alleen maar NU).
- De raaklijn Rj is voor Jan zijn X-as na een bepaalde tijd die hem bij S1 heeft
gebracht.
Dit is hoe Jan de wereld ziet.
Deze X-as is voor Jan zijn wereld van gelijktijdigheid, zijn beleving van het NU.
- De wereldlijn van Piet is zijn tijd-as,
hij kan dáár continu NU roepen, want elk punt op die lijn is
ook voor hem NU (ook in de werkelijkheid van Piet bestaat er uiteraard alleen maar NU).
- De raaklijn Rp is voor Piet zijn X-as na een bepaalde tijd die hem bij S2 heeft
gebracht.
Dit is hoe Piet de wereld ziet.
Deze X-as is voor Piet zijn wereld van gelijktijdigheid, zijn beleving van het NU.
Ik teken ook nog de asymptoot X
4 = X erbij in het plaatje.
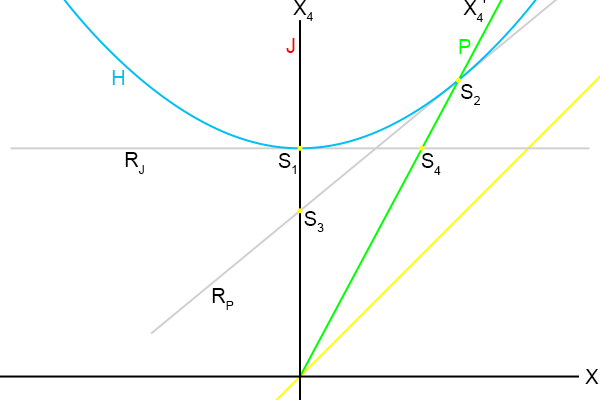
Figuur 4.16
En wat blijkt:
de hoek tussen de tijd-as en de asymptoot is altijd gelijk aan de hoek tussen de X-as en de asymptoot.
Met andere woorden: de som van de hoeken die tijd-as en X-as met een horizontale lijn maken is altijd 90 graden.
De
wereldlijn van Jan is verticaal,
de hoek met de asymptoot is dus 45 graden.
De X-as van Jan is horizontaal, de hoek met de asymptoot is dus ook 45 graden en de som van beide hoeken is inderdaad 90 graden.
De
wereldlijn
van Piet staat onder een bepaalde hoek met de horizontale as.
De
tangens
van die hoek is gelijk aan de richtingscoëfficiënt van de
wereldlijn van Piet: 1/β.
De X-as van Piet is de raaklijn R
p en deze maakt ook een bepaalde hoek met de horizontale as.
De
tangens
van deze hoek is gelijk aan de richtingscoëfficiënt van de raaklijn R
p: β.
Oftewel, de
tangens
van de ene hoek is 1/
tangens van de andere hoek.
Dus als de ene hoek φ graden is dan is de andere hoek (90 − φ) graden.
Waarmee bewezen is dat voor beide lijnen de hoek met de asymptoot gelijk is en dat de som van de hoeken weer 90 graden is.
En waarom merken wij niets van al deze gekkigheid (tijddilatatie e.d.) in onze alledaagse wereld?
Stel dat Piet vertrokken was bij Jan (figuur 4.6) op zijn fiets met een snelheid van 18 km/uur.
Een snelheid van 18 km/uur komt overeen met 5 m/s.
Daaruit volgt: β = 5/c = 5/299792458 = 1.67 ∙ 10
−8 =
tangens (hoek met de verticale as) ≈
hoek met de verticale as (de
tangens
van een hoek is nagenoeg gelijk aan de hoek zelf voor kleine hoeken).
De
wereldlijn
van Piet maakt dan een hoek van 1.67 ∙ 10
−8 radialen ≈ 0.3 nanograden (van radialen
naar graden is vermenigvuldigen met π/180) met de
wereldlijn van Jan!
In onze slome beleving vallen de wereldlijnen
van Jan en Piet gewoon samen.
In de voorgaande plaatjes met Jan en Piet, die ik getekend heb, is die hoek bijna 23 graden, dat levert een
tangens op van 0.421.
De snelheid van Piet is dus maar liefst 0.421 × 299792458 is meer dan 126 miljoen m/s = 126000 km/s!
Ter vergelijking: de
ontsnappingssnelheid
van de Aarde, de snelheid die ruimtevaartuigen moeten ontwikkelen om
de Aarde achter zich te laten en andere hemellichamen te bereiken, is ‘slechts’ 11 km/s.
Anno 2011 kunnen we van snelheden die een ‘beetje fatsoenlijke’ β opleveren alleen nog maar dromen, maar hier kon
ik niet anders omdat er bij realistische snelheden aan de hand van plaatjes simpelweg helemaal niets valt uit te leggen.
Voor de duidelijkheid volgt hieronder een tabel met snelheden en bijbehorende β en γ waarden.
| v [m/s] |
β |
γ |
| 0 |
0.000000000000000 |
1.000000000000000000000000000000 |
| 1 |
0.000000003335641 |
1.000000000000000005563250280268 |
| 3 |
0.000000010006923 |
1.000000000000000050069252522413 |
| 10 |
0.000000033356410 |
1.000000000000000556325028026810 |
| 30 |
0.000000100069229 |
1.000000000000005006925252241321 |
| 100 |
0.000000333564095 |
1.000000000000055632502802685564 |
| 300 |
0.000001000692286 |
1.000000000000500692525224504334 |
| 1000 |
0.000003335640952 |
1.000000000005563250280314516791 |
| 2998 |
0.000010000251574 |
1.000000000050002515775801110790 |
| 10000 |
0.000033356409520 |
1.000000000556325028491055521731 |
| 29979 |
0.000099999180099 |
1.000000004999918047780289223680 |
| 100000 |
0.000333564095198 |
1.000000055632507445144404197262 |
| 299792 |
0.000999998472276 |
1.000000499998847275631879421713 |
| 1000000 |
0.003335640951982 |
1.000005563296705329070770776895 |
| 2997925 |
0.010000001400969 |
1.000050003764324322042844724470 |
| 10000000 |
0.033356409519815 |
1.000556789705204583117680688046 |
| 29979246 |
0.100000000667128 |
1.005037815326938243295233855111 |
| 100000000 |
0.333564095198152 |
1.060752000444204002424507306501 |
| 299792457 |
0.999999996664359 |
12243.211557838899012388084642982317 |
| 299792458 |
1.000000000000000 |
∞ |
Of in grafiekvorm:
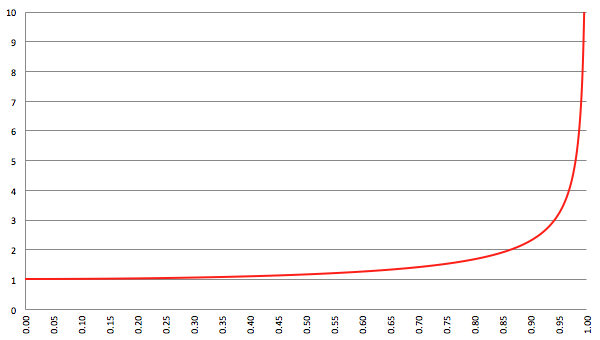
De grafiek van γ als functie van β
En ben ik nu eindelijk uitgepraat over Minkowski?
Nee, er is nog wat om te vertellen.
We roepen daarom onze waarnemers Jan en Piet er maar weer bij en we zetten ze gewoon ergens neer, op een willekeurige afstand
van r meter van elkaar.
En natuurlijk maak ik daar weer een plaatje van, want plaatjes zeggen zoveel meer.

Figuur 4.17
Nu willen we weten waar Piet precies staat ten opzichte van Jan.
Waarnemer Kees gaat dit voor ons uitzoeken.
Kees komt en brengt zijn eigen assenstelsel mee waarvan hij de oorsprong bij Jan neerlegt.
Hij gaat uitgebreid aan het meten, pakt daarna zijn boeltje in en vertrekt om zijn verslag te maken.
Voor de zekerheid vragen we een second opinion aan waarnemer Henk.
Ook Henk komt opdraven met zijn instrumentarium, legt ook de oorsprong bij Jan neer, en na gedane arbeid gaat ook hij zijn
verslag maken.
Uiteindelijk ontvangen we twee verslagen die we naast elkaar leggen.
| Verslag Kees |
Verslag Henk |
| De Y-as is referentie-as |
De Y-as is referentie-as |
| Piet staat op een afstand (r) van 6 meter van Jan |
Piet staat op een afstand (r) van 6 meter van Jan |
| De denkbeeldige lijn van Jan naar Piet staat onder een hoek (φk) van 50.0 graden |
De denkbeeldige lijn van Jan naar Piet staat onder een hoek (φh) van 27.5 graden |
| De denkbeeldige lijn van Jan naar Piet heeft een hellingsgetal (Hk) van 1.192 |
De denkbeeldige lijn van Jan naar Piet heeft een hellingsgetal (Hh) van 0.521 |
| De X-coördinaat van Piet (∆Xk) is 4.596 |
De X-coördinaat van Piet (∆Xh) is 2.770 |
| De Y-coördinaat van Piet (∆Yk) is 3.857 |
De Y-coördinaat van Piet (∆Yh) is 5.322 |
| Tabel 4.2 |
Heel fijn dat Kees en Henk in ieder geval dezelfde afstand gemeten hebben, maar verder kunnen we de resultaten niet direct rijmen.
Er zitten ook plattegronden bij de verslagen.
Dit is de plattegrond van Kees:
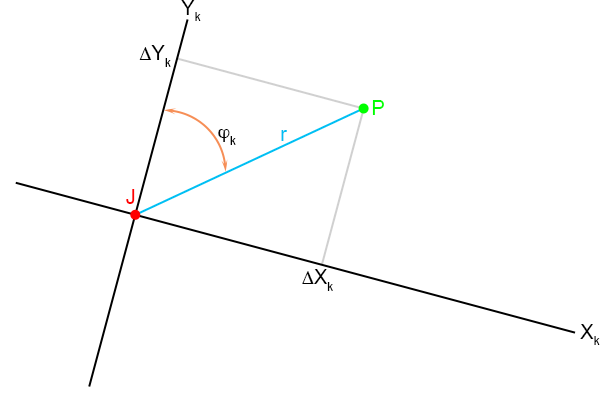
Figuur 4.18
En dit is de plattegrond van Henk:
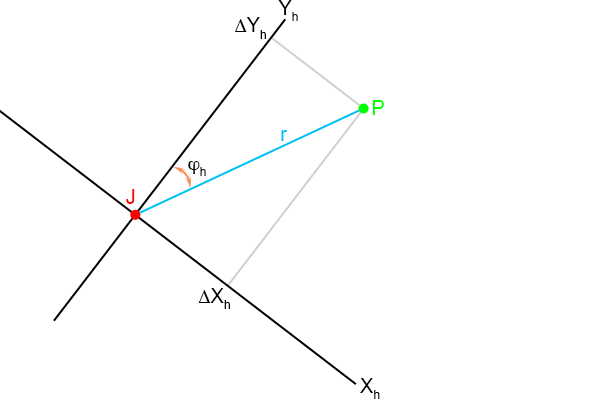
Figuur 4.19
Wat natuurlijk direct opvalt is dat de assenstelsels totaal verschillend zijn.
Daarom leggen we de plaatjes eens op elkaar.
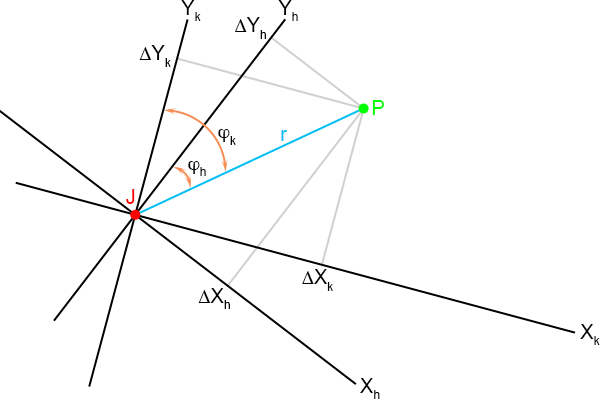
Figuur 4.20
Dit verklaart natuurlijk een hoop.
De assen van Kees en de assen van Piet zijn ten opzichte van elkaar gedraaid over een bepaalde hoek.
Die hoek noem ik ξ en die geef ik ook aan in het plaatje.
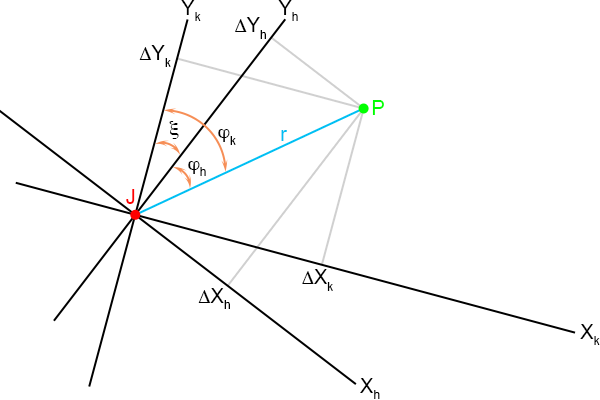
Figuur 4.21
Ik pak mijn gradenboog en meet de hoek ξ: 24.979 graden.
Dan begint alvast iets duidelijk te worden:
Met behulp van elementaire
goniometrie
is ook het volgende in te zien:
Voor beide stelsels geldt dan ook (
stelling van Pythagoras):
Dit klopt inderdaad, want Kees en Henk hebben beiden (uiteraard) dezelfde afstand r gemeten.
Maar hoe zijn die ∆X’en en ∆Y’en in elkaar om te rekenen?
Dat gaat zo:
Die overstap van het verschil van twee hoeken naar een product van
sinussen en
cosinussen gaat met behulp van een
hulpregel uit de
goniometrie,
en die zal ik ook nog even toelichten.
Ik moest daarvoor ook wel weer even puzzelen, maar via het onderstaande plaatje wordt het duidelijk (hoop ik) en zijn
de
sinus
en
cosinus van de somhoek (α + β) zo af te lezen.
De
sinus
en
cosinus
van de verschilhoek (α − β) verkrijg je door β te vervangen door −β,
en daarna de
sinussen
van β een minteken mee te geven.
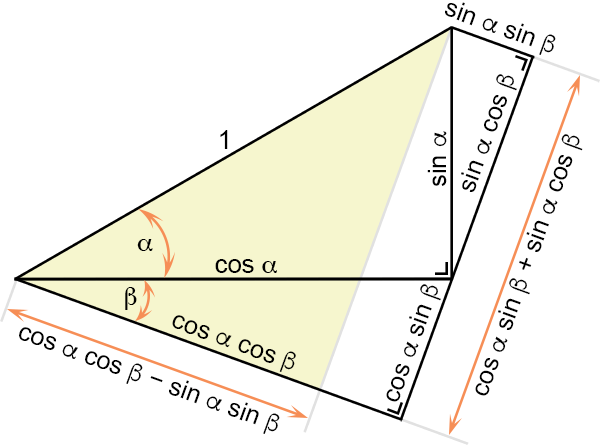
Figuur 4.22
Nu wil ik nog weten hoe de hellingsgetallen uit de verslagen van Kees en Henk in elkaar om te rekenen zijn.
Het hellingsgetal is de
tangens
van de hoek die die helling maakt.
De
sinus en de
cosinus kan ik schrijven als een
functie van de tangens:
Waaruit volgt:
De vergelijkingen (4.13c) en (4.13d) gaan we invullen in de vergelijkingen (4.12a) en (4.12b), waarbij we ook nog gebruik maken van:
Dit is dan de afleiding:
En H
h vinden we dan door de vergelijkingen (4.15a) en (4.15b) op elkaar te delen.
Indien we alleen het verslag van Kees hadden ontvangen, en een andere waarnemer had ons verteld dat het assenstelsel van Henk een hoek
ξ maakte met het assenstelsel van Kees, dan hadden we de meetgegevens van Henk als volgt kunnen uitrekenen:
- Volgens vergelijking (4.9) is de hoek φh uit te rekenen.
- Volgens vergelijking (4.16) is het hellingsgetal Hh uit te rekenen.
- Volgens vergelijking (4.12a) is de X-coördinaat ∆Xh uit te rekenen.
- Volgens vergelijking (4.12b) is de Y-coördinaat ∆Yh uit te rekenen.
Aan jou de eer om te controleren of het ook inderdaad allemaal klopt, dus pak je rekenmachine!
En nu ga ik nog één keer terug naar de ‘cirkel’ (de hyperbolen) van Minkowski.
Ik neem het plaatje van figuur 4.12, met de
wereldlijnen
van Jan en Piet, en voeg daar nog een derde
wereldlijn
aan toe.
Ook geef ik wat hoeken aan, en dan ziet het er zo uit:
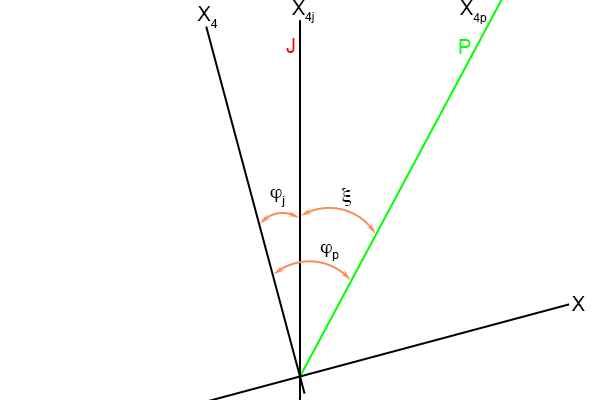
Figuur 4.23
Piet beweegt naar ‘rechts’ ten opzichte van Jan, en zowel Jan als Piet bewegen naar ‘rechts’ ten opzichte van een bepaalde
referentie-as X
4.
En “rechts” staat wederom tussen quotes, want in dit tweedimensionale plaatje worden vier dimensies uitgebeeld.
Wat er op dit plaatje uitziet als “rechts” kan in werkelijkheid wel een beweging naar achteren zijn en tegelijkertijd omhoog.
De derde
wereldlijn is een of andere X
4 referentie-as.
Ik heb alleen de X-as getekend behorend bij de X
4 referentie-as.
Het wordt daardoor wel een beetje een raar plaatje, maar dit is relativiteitstheorie, dus waarom moeten de assen van een
assenstelsel zo nodig precies horizontaal of verticaal staan?
De X-assen van Jan en Piet heb ik weggelaten, want die X-assen voegen nu even niets toe.
Nu gaan we de doos met wiskundige trucs er maar eens bij pakken.
Wat is de
wortel uit een negatief getal?
Dat kan niet hebben we geleerd, maar wiskundigen zijn niet voor een gat te vangen en hebben daarom de volgende
oplossing bedacht, de
imaginaire eenheid i:
De
wortel uit bijvoorbeeld −49 is:
Verder wil ik hier de
hyperbolische functies introduceren:
Waaruit volgt dat:
En ook:
En maak kennis met de vergelijkingen van Euler (naar Leonhard Euler, een Zwitsers wiskundige):
Het getal e heet het getal van Euler.
Door optelling respectievelijk aftrekking van de vergelijkingen (4.19a) en (4.19b) ontstaan:
Hiermee gaan we aan de slag om vergelijking (4.2) te verbouwen.
En dit is de normale vergelijking van een cirkel!
Weliswaar met een imaginaire component erin, maar dat mag de pret niet drukken.
En voor een cirkel gelden de
goniometrische
regels van vergelijking (4.10), dus dat doen we hier ook.
Ik gebruik hier de indices j en p van Jan en Piet.
En dit combineren we met de vergelijkingen (4.20a) en (4.20b):
Dezelfde afleiding voor Piet levert dan uiteraard op:
En voor de andere coördinaat levert dit op:
En tenslotte vormt zich hieruit tanh (−iφ), en dit geldt dan uiteraard zowel voor Jan als voor Piet.
Nu vervang ik de negatieve imaginaire hoek −iφ door Ψ (niet bij nadenken, gewoon doen).
Ook hier is dit op zowel Jan als Piet van toepassing.
Als ik hiermee aan de gang ga, net als in vergelijking (4.11), dan levert dat het volgende op:
Analoog aan vergelijking (4.9) geldt hier:
En we kunnen uiteraard ook coördinaten omrekenen zoals we met vergelijking (4.12) uitgezocht hebben.
Dus dat gaan we nu ook doen:
En net zoals de gewone
sinus en
cosinus te schrijven zijn als een
functie van de tangens (zoals in vergelijking (4.13)), zo zijn ook de
sinus hyperbolicus en
cosinus hyperbolicus te schrijven als een
functie van de tangens hyperbolicus:
Waarna we deze wijsheid gebruiken en in de vergelijkingen (4.28a) en (4.28b) stoppen:
Indien we ook nog bedenken dat:
Dan veranderen de vergelijkingen (4.30a) en (4.30b) in:
En hieruit distilleren we β
p:
Hier staat ineens de formule voor het relativistisch optellen van snelheden!
Via de hyperbolen van Minkowski en wat negatieve imaginaire hoeken kunnen we uiteindelijk zelfs de
Lorentz-transformaties (vergelijkingen (4.30)) weer tevoorschijn halen.
Is relativiteitstheorie (en wiskunde) leuk of niet?
Een goed moment om alles wat we hiervoor allemaal hebben uitgewerkt nu bij elkaar te zetten in een tabel.
| Ruimte |
Ruimtetijd |
Afstand:
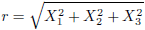 |
Afstand (interval):
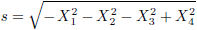 |
Afstand:
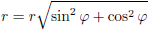 |
Afstand (interval):
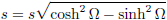 |
Positie (hellingsgetal):
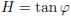 |
Snelheid (hellingsgetal):
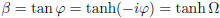 |
Rotatiehoek:
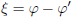 |
Rotatiehoek:
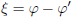 |
Positie (hellingsgetal) na rotatie:
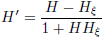 |
Snelheid (hellingsgetal) na rotatie:
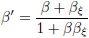 |
Coördinaat X1 na rotatie:
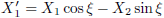
(bij rotatie in het X1-X2-vlak) |
Coördinaat X1 na rotatie:
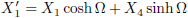
(bij rotatie in het X1-X4-vlak) |
Coördinaat X2 na rotatie:
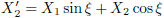
(bij rotatie in het X1-X2-vlak) |
Coördinaat X4 na rotatie:
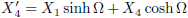
(bij rotatie in het X1-X4-vlak) |
| Tabel 4.3 |
Even een hele belangrijke opmerking: dit laatste stuk stond bol van de wiskundige trucs.
Dus ren nu niet gelijk naar je moeder of naar wie dan ook om te roepen dat er imaginaire tijd bestaat, want
die bestaat alleen in onze wiskundige fantasie.
In de wiskunde mag je de gekste abstracties bedenken en toepassen, als je uiteindelijk dan maar wel weer met beide
benen op de grond belandt.
Dit moest echt allemaal ‘even’ gezegd worden over Minkowski en zijn elegante wiskundige bouwwerk.
Daarom: hulde aan Minkowski!
Ik haal nu vergelijking (4.2) er weer bij waar ik dit hele verhaal zo ongeveer mee begon.
Maar als we het artikel van Einstein bekijken dan zien we daar iets fundamenteel anders staan:
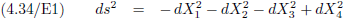 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
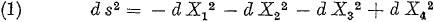
Opmerking: de aanduiding “/E1” voor de vergelijking refereert aan het nummer van de desbetreffende vergelijking in het artikel
van Einstein.
In dit geval is dit dus zijn eerste vergelijking.
Voor de schuine streep staat het volgnummer dat ik aan de vergelijking heb gegeven.
En om het cultureel-historische besef van wat we aan het doen zijn wat op te krikken voeg ik de originele vergelijking van
Einstein toe uit het oorspronkelijke Duitse artikel.
Wat is er aan de hand?
In alles wat ik hiervoor verteld heb gingen we uit van
constante snelheden, dat is ook de beperkende factor
van de speciale relativiteitstheorie.
Maar in de echte wereld zijn er natuurlijk niet alleen maar constante snelheden, er zijn ook versnellingen.
Kijk maar eens naar het volgende plaatje met twee
wereldlijnen van Jan respectievelijk Piet.
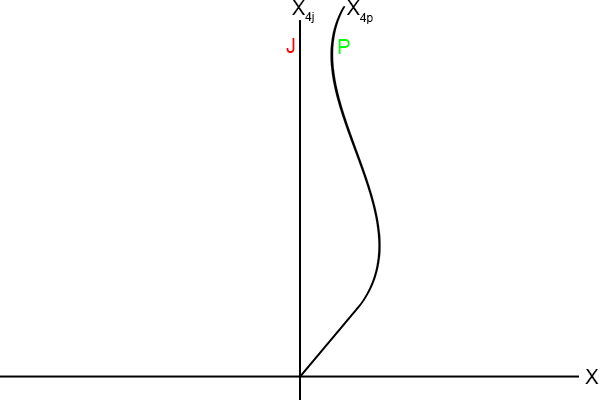
Figuur 4.24
Jan bevindt zich continu op dezelfde positie, hij staat een patatje te eten of zoiets, of hij ligt in bed.
Maar Piet is volop in beweging, het ene moment beweegt hij naar ‘rechts’, dan weer naar ‘links’.
Hij versnelt, hij vertraagt en ook staat hij weleens stil (allemaal ten opzichte van Jan uiteraard).
De raaklijnen aan de kromme van zijn
wereldlijn
‘verraden’ wat hij aan het doen is.
Op deze momenten staat Piet bijvoorbeeld stil (ten opzichte van Jan):
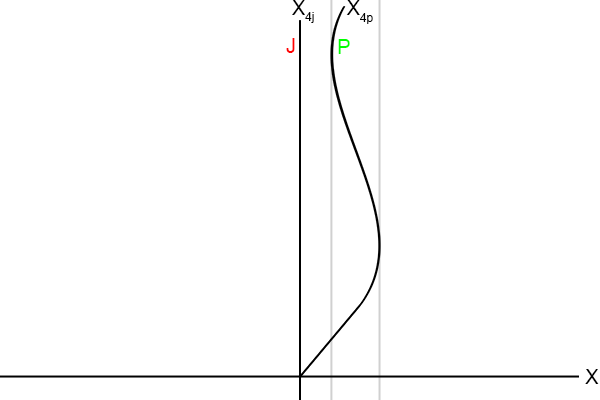
Figuur 4.25
En op deze momenten beweegt Piet (ongeveer) met constante snelheid (ten opzichte van Jan):
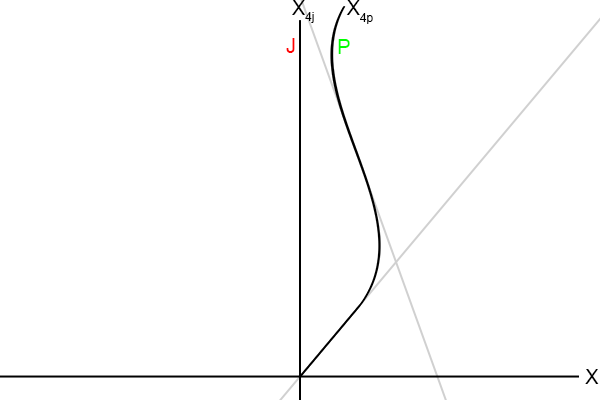
Figuur 4.26
En op alle overige momenten is Piet vooral aan het remmen of gas geven.
Maar Einstein merkt op dat wanneer je de
wereldlijn
van Piet op een heel klein stukje (“oneindig klein”) beschouwt,
dat daar de snelheid
wel constant is.
En voor constante snelheden geldt de speciale relativiteitstheorie.
Met andere woorden: als je van de ene gebeurtenis (ik kan het niet vaak genoeg zeggen: elk punt in de grafiek is een
gebeurtenis!) naar de meest nabijgelegen gebeurtenis ‘overspringt’, dan overbrug je een oneindig klein ruimtetijdintervalletje.
En “oneindig klein” geven we aan met de letter d, dus het interval wordt dan ds.
En de
wereldlijn van Piet kun je zien als een
aaneenschakeling van oneindig veel oneindig kleine raaklijntjes, maar al die
oneindig kleine raaklijntjes zijn wel oneindig kleine intervalletjes waar de snelheid constant is.
Dus door vergelijking (4.2) toe te passen op het oneindig kleine gaat die vergelijking over in vergelijking (4.34/E1) en kan die op
elk punt van de wereldlijn
(“plaatselijk” noemt Einstein dat) van Piet toegepast worden.
En daar waar de snelheid constant is, daar is de versnelling nul, dus daar treden geen krachten op die op Piet inwerken.
In
paragraaf 2
hebben we het uitgebreid gehad over het
equivalentieprincipe en daarom kunnen we stellen: dan is er in dat
geval ook geen zwaartekrachtveld werkzaam.
En dit is waar Einstein naar toe wil (denk ik) in deze paragraaf: als je uitgaat van oneindig kleine vierdimensionale gebieden
dan treedt er geen zwaartekrachtveld op.
Verder merkt hij nog op dat de beschrijving van het interval volgens vergelijking (4.34/E1) een
directe betekenis heeft in
de echte wereld, in de werkelijkheid.
Een oneindig kleine verplaatsing dX
1 naar rechts of naar links, of een oneindig kleine verplaatsing dX
2
naar voren of naar achteren, of een oneindig kleine verplaatsing dX
3 naar boven of naar beneden, is rechtstreeks
te meten met een oneindig kleine lineaal.
En een oneindig kleine ‘verplaatsing’ dX
4 in de tijd is te meten met een klok die dat hele kleine beetje tijd
kan meten.
Hoe dat praktisch te realiseren is daar gaat het nu niet om, het belangrijkste is dat er een één-op-één relatie is tussen
de vergelijking en de werkelijkheid.
Op die manier kunnen we ons voor ogen houden waar we mee bezig zijn, en dat is wel zo prettig.
En met behulp van onze waarnemers Jan en Piet hebben we hiervoor uitgebreid uitgeplozen hoe een bepaald ruimtetijdinterval door
hen beiden ervaren wordt: het is gelijk.
Net zoals de waarnemers Kees en Henk voor ons hebben duidelijk gemaakt dat een ruimtelijke afstand onafhankelijk is van de waarnemer,
oftewel, onafhankelijk is van het assenstelsel waarin de ruimtelijke afstand gemeten wordt.
En dit geldt echt voor elk assenstelsel.
Bekijk eens even het volgende plaatje (voor de duidelijkheid in twee dimensies getekend).
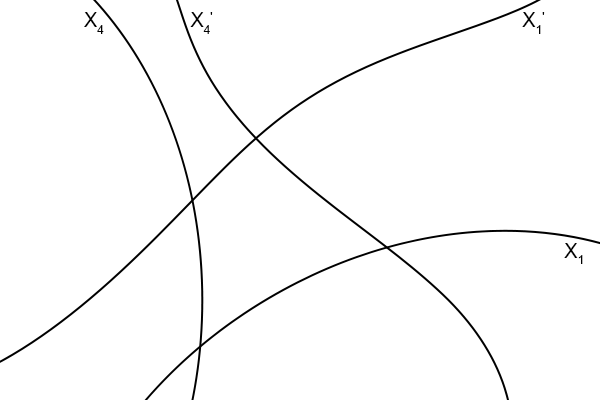
Figuur 4.27
Want nergens staat geschreven dat assen recht moeten zijn, dat doen we doorgaans wel maar dat is puur voor ons eigen gemak.
Maar de assenstelsels in figuur 4.27 zijn net zo geldig als elk ander.
Ik teken er ook even twee gebeurtenissen bij in die oneindig dicht bij elkaar liggen.
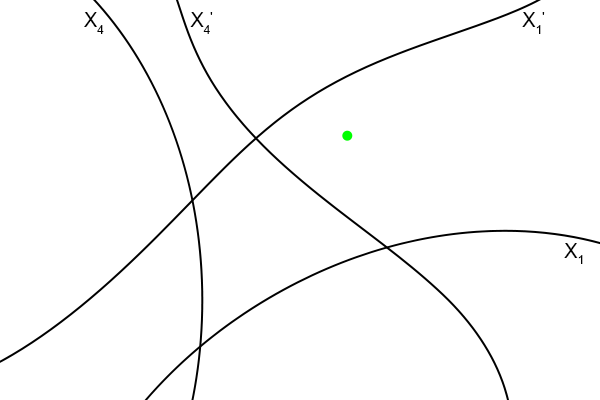
Figuur 4.28
Precies, die twee gebeurtenissen zijn samen één stip omdat ze oneindig dicht bij elkaar liggen.
Laten we daarom maar eens flink inzoomen.
In onze fantasie pakken we een microscoop met een vergroting van ongeveer oneindig, en dan zien we dit:
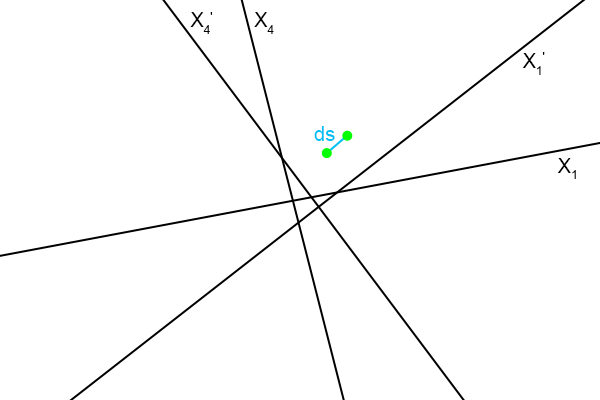
Figuur 4.29
Daar,
ter plaatse van het oneindig kleine, zijn de assen recht.
Althans, de oneindig kleine delen van de assen die we door de supermicroscoop zien.
En dat hele kleine stukje ds, de afstand van de ene gebeurtenis naar de andere, is vanuit beide assenstelsels gemeten gelijk
(uiteraard).
Dus als we maar in het oneindig kleine een
wereldlijn beschouwen, dan ‘zien’ we een
ruimtetijdintervalletje dat onafhankelijk is vanuit welk stelsel er gemeten wordt.
Oftewel, in het oneindig kleine kun je een heel klein assenstelsel bedenken (“lokaal” noemt Einstein dat), waarvan het niet
uitmaakt hoe het georiënteerd is, en vervolgens kunnen we daar het ruimtetijdintervalletje opmeten.
Het ruimtetijdintervalletje ds is namelijk invariant, dus ongeacht vanuit welk assenstelsel er gemeten wordt: ds is altijd
hetzelfde.
Mede daarom heeft Einstein net nog expliciet vermeld dat dat ruimtetijdintervalletje werkelijk bestaat en met behulp van
meetlatten en klokken op te meten is.
Zo dicht mogelijk bij de werkelijkheid blijven is het motto van Einstein, want voordat je er erg in hebt gaat je brein van
alles bedenken wat er helemaal niet is en dat willen we niet.
Daar is je brein namelijk heel erg goed in, om met allerlei
illusies
op de proppen te komen.
En in dat oneindig kleine vierdimensionale gebiedje is de snelheid constant en is dus ook de speciale relativiteitstheorie
van toepassing.
Er is één kleine, maar hele belangrijke en vervelende, ‘oeps’: de assen staan niet loodrecht op elkaar.
Indien de assen wel loodrecht op elkaar staan dan is het leven zo heerlijk simpel en kunnen we met behulp van de
stelling van Pythagoras
de afstand tussen twee punten uitrekenen.
Daarom is het de hoogste tijd om weer eens in de wiskundige trucendoos te graaien.
En wat komt daar uit?
Vectoren!
De Nederlander Willebrord Snel van Royen kwam als eerste met het concept van een vector.
Maar wat is een vector?
Vectoren zijn voorstellingen van ‘iets’ dat een richting heeft in tegenstelling tot een scalar die ‘iets’ voorstelt zonder richting.
Een scalar is simpelweg een getal, bijvoorbeeld de temperatuur.
Wanneer ik zeg dat de temperatuur hier twintig graden celsius is dan ben ik volledig duidelijk.
Maar wanneer ik zeg dat ik fiets met een snelheid van achttien km/uur dan is de voor de hand liggende vraag: waarheen dan?
Snelheden hebben dus een grootte (in dit geval achttien km/uur) en een richting.
Vectoren worden voorgesteld door pijltjes, en deze pijltjes hebben een grootte en een richting.
Scalaire grootheden (zoals temperatuur) worden volledig weergegeven door een getal.
Vectoriële grootheden (zoals snelheid) worden volledig weergegeven door een getal én een richting.
Indien ik een bepaalde kant op fiets dan kan ik dat aangeven met een pijltje (vector) die in die richting wijst.
En als mijn snelheid 18 km/uur (= 5 m/s) bedraagt dan kan ik dat pijltje bijvoorbeeld een lengte meegeven van 5 cm.
Ik kan erbij zetten dat het om een snelheid gaat door er v bij te schrijven, en de “v” wordt vet gedrukt om
aan te geven dat het een vector is.
Dat ziet er dan zo uit:
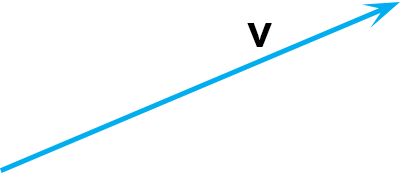
Figuur 4.30
De vector in figuur 4.30 wijst naar rechts, maar ook een stukje omhoog.
Indien ik hier een X-Y-assenstelsel bij denk dan heeft de vector
v dus een X-deel en een Y-deel.
Dit noemen we de
componenten van de vector
v en dat schrijven we als volgt op:
v (v
x, v
y).
Of in drie dimensies:
v (v
x, v
y, v
z).
De componenten van de vector mag je trouwens ook boven elkaar schrijven en dan de komma’s weglaten.
Verder wil ik nog opmerken dat vectoren niet gebonden zijn aan een coördinatenstelsel
(zolang we het puur over de vector zelf hebben en niet over de componenten van
die vector, want de componenten vormen de verbinding met het coördinatenstelsel), en omdat we bezig zijn met relativiteitstheorie
is dit een hele belangrijke.
Pas op het moment dat ik begin te praten over de componenten van een vector verbind ik mij met een coördinatenstelsel.
In onze wiskundige fantasie kan van alles door vectoren voorgesteld worden: snelheden, krachten, veldsterkte, verplaatsingen, enzovoort.
Dit gaan we gebruiken om het probleem van figuur 4.29 aan te pakken.
We zoomen nog wat verder in en we beperken ons even tot één assenstelsel.
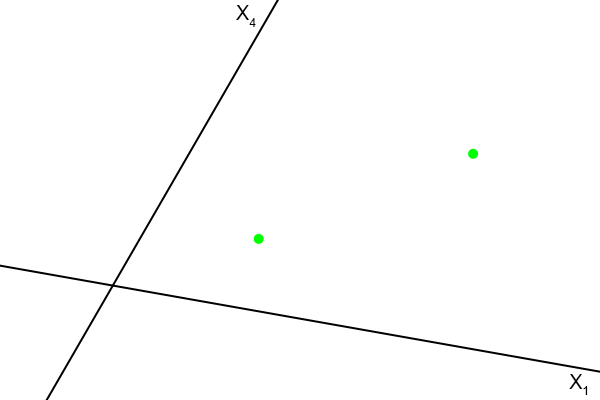
Figuur 4.31
We beschouwen twee gebeurtenissen, die noemen we G
1 en G
2.
En de ruimtetijdafstand tussen de beide gebeurtenissen, die oneindig dicht bij elkaar liggen, is ds.
Dat schrijf ik er even bij in het plaatje.
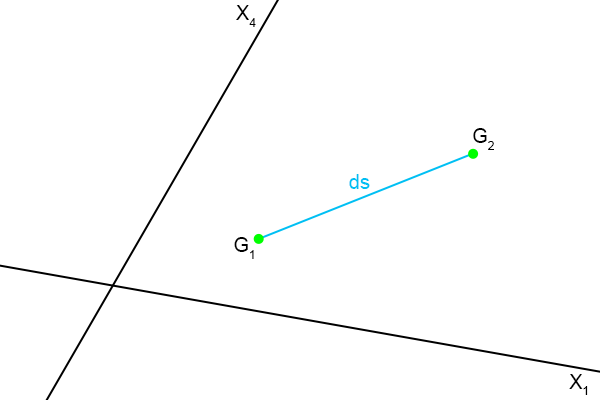
Figuur 4.32
Als ik van gebeurtenis G
1 naar gebeurtenis G
2 ga dan beweeg ik in de X
1-dimensie, maar tegelijkertijd
ook in de X
4-dimensie.
Die bewegingen ga ik ook in het plaatje erbij tekenen als
vectoren.
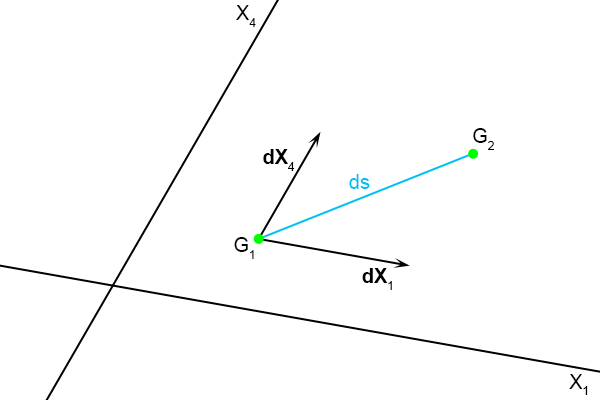
Figuur 4.33
Hierin is ds nog steeds ‘gewoon’ de grootte van het lijnstukje tussen G
1 en G
2, maar
dX1
en
dX4 zijn vectoren en dus
vet gedrukt.
De verplaatsing in de X
1-dimensie is voorgesteld door de vector
dX1 en de verplaatsing in de
X
4-dimensie is voorgesteld door de vector
dX4.
De vector
dX1 loopt daarom ook parallel aan de X
1-as en de vector
dX4 loopt parallel
aan de X
4-as.
Vectoren kun je bij elkaar optellen en dit is te visualiseren door ze kop-aan-staart te leggen.
Daarom verplaatsen we
dX4 en leggen die bij de pijlpunt van
dX1 als volgt:
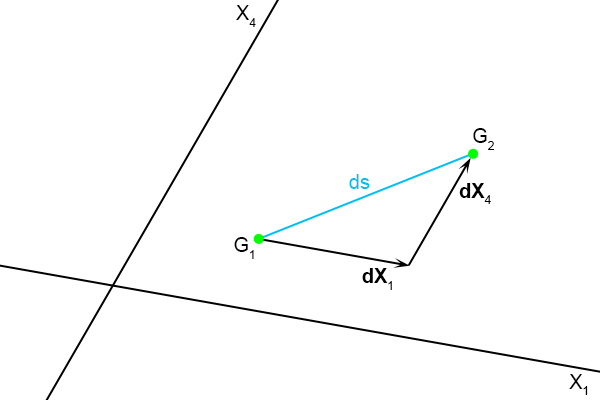
Figuur 4.34
En als vergelijking ziet dat er dan zo uit (let op:
ds is hier een vector(tje)!):
Volgende truc: we gaan het
inwendig product
nemen van het vectortje
ds met
zichzelf.
In hoofdstuk B van het artikel van Einstein wordt de hele benodigde wiskunde blootgelegd en daar leg ik ook in detail uit wat
het
inwendig product is en doet.
Daar is het beter op zijn plaats, want dan vormt de uitleg één geheel met het
uitwendig product en het tensor product
en nog veel meer wiskundige uitleg, en daarom ga ik er hier niet verder op in.
Bovendien is deze paragraaf 4 nu al zo omvangrijk, terwijl we natuurlijk ook niet alles tegelijk moeten willen.
Voor de ongeduldigen: kijk dan maar alvast in de uitleg van
paragraaf 6.
Ik ga intussen verder met de
inwendig-product-truc.
De trucendoos is nog lang niet leeg.
Het vectortje
dX kan ik ook anders schrijven.
Stel het vectortje
dX is een miljoenste meter, dan kan ik ook een vector nemen van exact één meter en daar een miljoenste
voor zetten als volgt: dx
X.
De vector
X is hier dus een
eenheidsvector, de lengte is één, en normaliter wordt dat aangegeven met een ‘dakje’
boven de vector.
Uiteindelijk heb ik dan toch weer een vectortje van een miljoenste meter, dus zowel grootte als richting blijven onaangetast.
Dit ga ik toepassen in vergelijking (4.36).
De uitkomst van een
inwendig product is per definitie een getal.
Dus die vier
inwendige producten
X ∙
X die hierboven staan leveren vier getallen op.
Zo’n getal noem ik g en ik geef er indices aan om ze uit elkaar te houden.
Ik heb het hier uitgewerkt in twee dimensies, X
1 en X
4, maar het kan natuurlijk ook in drie dimensies.
Daarvoor ga ik niet weer in detail alle stappen doornemen, ik schrijf alleen het eindresultaat op:
En je voelt het al aankomen: de uitbreiding naar vier dimensies:
Dit vráágt gewoon om een meer systematische formulering.
Als ik hierbij de indices σ en τ introduceer dan kan ik ook schrijven:
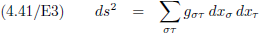 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
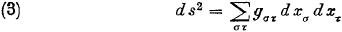
Waarbij σ en τ onafhankelijk van elkaar achtereenvolgens de waarden 1, 2, 3, 4 doorlopen.
Deze manier van afstanden beschrijven in gekromde dimensies is onderdeel van de differentiaal meetkunde of
differentiaal geometrie.
De grondlegger hiervan is Carl Friedrich Gauss en daarom vallen er ook weleens kreten als Gaussische coördinaten
of Gaussische meetkunde.
Als je in verband met relativiteitsheorie de naam Gauss hoort vallen dan is dat gegarandeerd als tegenhanger van Euclides.
De meetkunde van de Griek Euclides betreft niet-gekromde vlakken, terwijl voor Gauss totaal geen restricties bestaan.
Een leerling van Gauss, Bernhard Riemann, heeft voortgeborduurd op het werk van Gauss, en het werk van Riemann diende op zijn beurt weer
als fundament voor het werk van Einstein.
Zonder de genialiteit van Riemann geweld aan te willen doen, was het toch echt Gauss die aan de basis stond van de
differentiaal geometrie.
Daarom: hulde aan Gauss!
Echter, om niemand tekort te doen wil ik hier in dit verband ook graag de Hongaar János Bolyai en de Rus Nikolai Ivanovich Lobachevsky vermelden.
Deze twee mannen hebben, onafhankelijk van Gauss en onafhankelijk van elkaar, eveneens baanbrekend werk verricht op het gebied van de
differentiaal geometrie.
Zoals met zoveel zaken die vanuit een westers standpunt ‘niet passen’ wordt dat ‘gemakshalve’ vaak over het hoofd gezien.
Daarom bij deze ook expliciet hulde aan Bolyai en Lobachevsky!
Verder is het zo dat het niet uitmaakt of je het
inwendig product
uitrekent van
A ∙
B of
B ∙
A
(dit heet
commutatief), de uitkomst blijft exact gelijk.
Maar dat betekent dan wel dat:
Oftewel, de 16 g
στ componenten hebben altijd maximaal 16 − 6 = 10 verschillende waarden.
Of zoals Einstein het zegt: 12 g
στ componenten zijn paarsgewijs gelijk.
Als ik de 16 g
στ componenten even netjes en logisch en overzichtelijk opschrijf dan ziet dat er zo uit:
Deze tabel staat bekend als de
metrische tensor,
of kortweg de
metriek, en is één van de bouwstenen van
de algemene relativiteitstheorie.
Over deze tensor is heel veel te vertellen, maar de essentie is:
hij is ‘los’ van coördinaten
(en net als bij de vectoren geldt ook voor de tensoren: de tensor is onafhankelijk van coördinatenstelsels, maar de componenten
niet, de componenten vormen de verbinding met een coördinatenstelsel).
Ik voel inmiddels de vraag bij je branden: wat is in vredesnaam een tensor?
Logisch, dat had ik ook de eerste keer dat ik mij verdiepte in deze materie.
Neem voor het moment gewoon even aan dat die zestien dingetjes van vergelijking (4.42) er zijn om de afstand ds te beschrijven.
Punt.
In
paragraaf 6 kom ik uitgebreid terug op wat een tensor is,
dus heb nog even geduld.
Vergelijking (4.41/E3) beschrijft de afstand ds van gebeurtenis G
1 naar gebeurtenis G
2 op eenduidige wijze en
het maakt daarbij helemaal
niet uit hoe mijn assenstelsel eruit ziet.
Altijd, maar dan ook altijd, kan ik stellen dat vergelijking (4.41/E3) de afstand ds beschrijft.
Dit kan ik niet genoeg benadrukken, dit is de kracht van de tensor.
Verderop in het artikel besteedt Einstein een hele paragraaf
(
paragraaf 8) aan de metrische tensor, dus daar gaan we het
nog uitgebreid over deze tensor hebben.
De metrische tensor in algemene relativiteitstheorie wordt altijd aangegeven met indices μ en ν: g
μν.
Deze tensor heeft ook een diagonaal.
En met de diagonaal bedoel ik hier de
hoofddiagonaal
die van linksboven naar rechtsonder loopt.
De andere diagonaal die van rechtsboven naar linksonder loopt is de
nevendiagonaal.
De 6 componenten boven de
hoofddiagonaal
zijn gelijk aan de 6 componenten onder de
hoofddiagonaal, met andere woorden: de metrische
tensor is
symmetrisch (spiegelsymmetrie ten opzichte van de
hoofddiagonaal).
Wanneer de assen van een assenstelsel niet loodrecht op elkaar staan en/of de assen zijn niet kaarsrecht en/of de maatverdeling
op de assen is niet overal gelijk, dan ontkom je er niet aan om de metrische tensor aan boord te halen.
In het volgende hoofdstuk (hoofdstuk B) ga ik het uitgebreid hebben over tensoren en ‘hoe die dingen werken’.
Wat verder nog belangrijk is om op te merken: die 16 g
στ componenten zijn bepaalde
getallen wanneer
de assen recht zijn en een constante maatverdeling hebben.
Wanneer ik enkel naar dat stukje ds van figuur 4.32 kijk dan kan ik daar 16 getalletjes bij schrijven die
daar ter plekke de metrische tensor vormen.
Laten we dat dan maar eens doen.
Daarom hier de definitie van het
inwendig product:
Omdat ik hierboven uitgegaan ben van eenheidsvectoren is |
X | gelijk aan 1.
Het
inwendig product
van twee eenheidsvectoren is dan simpelweg cos φ, de
cosinus van de hoek die de beide vectoren met elkaar maken.
Als ik die wijsheid gebruik en nogmaals naar vergelijking (4.38) kijk, dan is g
11 = g
44 = 1 (want de hoek tussen een
vector en zichzelf is 0 graden en dus is de
cosinus 1).
En g
14 = g
41 = cos φ.
Vergelijking (4.38) wordt dan:
Die hoeken φ en θ teken ik er snel even bij in in figuur 4.34.
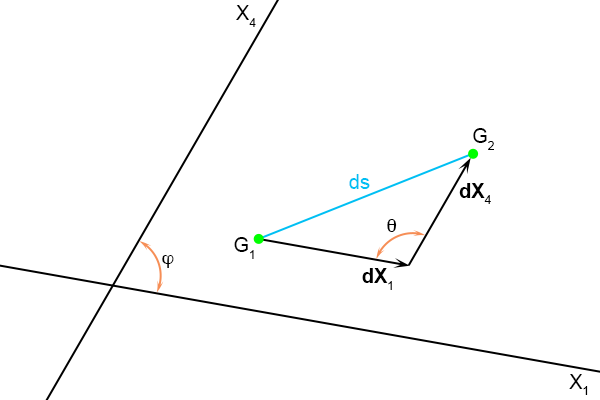
Figuur 4.35
En als je dan kijkt naar vergelijking (4.45) dan zie je de ...
cosinusregel!
Ja, denk maar even goed na, want die heb je vast wel gehad bij wiskunde.
En indien de assen loodrecht op elkaar staan dan is de hoek tussen de vectoren 90 graden en de
cosinus is dan 0.
De laatste term valt dan uit vergelijking (4.44) (en (4.45)) en daarmee reduceert vergelijking (4.44) (en (4.45)) tot de
stelling van Pythagoras.
Wat zit de wiskundige wereld toch mooi in elkaar!
Uiteindelijk ziet de tabel van de metriek, de metrische tensor, er dan zo uit:
Dit vraagt nog wel om wat toelichting:
- Ten eerste zie je hier heel duidelijk dat wanneer alle assen loodrecht op elkaar staan de metriek versimpelt
tot een hoofddiagonaal die gevuld is met enen
en voor de rest uit nullen bestaat.
Alle gστ componenten zijn dan nul voor σ ≠ τ.
- Ten tweede hebben we hier de metriek bepaald op één punt in de ruimtetijd, namelijk de overgang van gebeurtenis
G1 naar G2.
Het is echter heel goed mogelijk dat de metriek een stukje verderop heel anders is.
De 16 gστ componenten zijn in die gevallen geen getallen, maar functies van x1,
x2, x3 en x4 die hun waarde in elk punt van de ruimtetijd aangeven.
- Ten derde zie je hier op de hoofddiagonaal
allemaal positieve enen staan, terwijl we in deze paragraaf uitgebreid het interval s2 bestudeerd hebben
waarbij de ruimtelijke coördinaten een minteken met zich meedroegen (zie vergelijking (4.2)).
Het interval ds van figuur 4.32 heb ik wiskundig helemaal uitgewerkt alsof X1 en X4 ‘gewone’
ruimtelijke dimensies zijn, maar in relativiteitstheorie is dat allerminst het geval.
Wanneer ik X4 vervang door ict, dan wordt X42 gelijk aan −c2t2
en ontstaat het ruimteachtige interval (zie vergelijking (4.7)).
Indien het mij gaat om het tijdachtige interval (en daar gaat het mij om) dan zal ik
de gehele metrische tensor met −1 moeten vermenigvuldigen.
- Ten vierde heb ik in dit voorbeeld met slechts twee dimensies gewerkt.
Van de beide andere dimensies heb ik gemakshalve aangenomen dat daar de assen keurig loodrecht op elkaar staan en er geen
andere ‘gekke dingen’ aan de hand zijn.
Wanneer ik al deze wijsheid meeneem en vervolgens de metrische tensor opschrijf voor een tijdachtig interval waarbij de assen
loodrecht op elkaar staan, dan wordt dat:
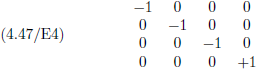 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
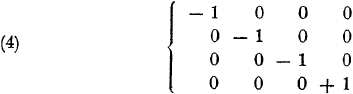
Deze metriek wordt ook wel aangeduid als de
Minkowski-metriek of de metriek van een
vlakke ruimte.
Wat er met dat laatste bedoeld wordt komt zo aan de orde, maar in ieder geval heeft men deze metriek een apart symbool
toebedacht: η
μν.
Einstein doet deze hele afleiding trouwens anders.
Hij zegt: de
differentialen
van de coördinatenstelsels zijn door
lineaire homogene vergelijkingen
met elkaar verbonden.
Wat bedoelt hij daar nou weer mee?
Stel, ik verplaats mij binnen het ene stelsel een heel klein stukje in de x-richting en mijn y-coördinaat en z-coördinaat
blijven ongewijzigd.
In het andere stelsel hoeft dat uiteraard helemaal niet zo te zijn, dat zou alleen waar zijn indien alle assen van beide
stelsels parallel lopen en dezelfde schaalverdeling hebben.
Kortom, mijn verplaatsing in de x-richting is in het andere stelsel misschien wel een verplaatsing in de y-richting of een
combinatie van y-richting en z-richting.
Maar aangezien we in het oneindig kleine bezig zijn is alles recht, zie figuur 4.35, en recht is in wiskundige taal lineair.
Of wat formeler uitgedrukt: alle variabelen in een lineaire vergelijking hebben een exponent die gelijk is aan één en
behalve de variabelen komen er alleen constanten voor in de vergelijking (dus geen
logaritmes,
sinussen, enzovoort).
Bijvoorbeeld de vergelijking y = ax is een lineaire vergelijking, want als je een grafiek maakt van y als functie van x
dan ontstaat een rechte lijn.
Dus een stukje dX in het ene stelsel laat zich niet beschrijven met allerlei moeilijke wiskundige vergelijkingen
(
wortels,
logaritmes,
kwadraten,
e-
machten, enzovoort)
in het andere stelsel, maar heel eenvoudig als:
En dit kunnen we uiteraard uitbreiden voor alle vier dimensies.
Maar de α
1 van vergelijking (4.48a) hoeft natuurlijk helemaal niet gelijk te zijn aan de α
1
van vergelijking (4.48b) (of (4.48c) of (4.48d)).
Dat moeten we even duidelijk maken middels een extra index.
De exponent, de
macht,
van alles wat we in vergelijking (4.49) zien is één, dus er staat nergens een
kwadraat of een derde
macht
of een
wortel.
Alles is geschreven tot-de-
macht-één,
alle exponenten zijn dus gelijk.
Dit noemen we
homogeen, vergelijking (4.49) is een homogene vergelijking van dx (als er ergens een α
2
had gestaan dan was er nog steeds sprake van een homogene vergelijking van dx maar niet meer van α).
En vergelijking (4.49) kunnen we natuurlijk veel systematischer opschrijven.
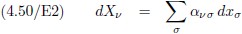 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Vergelijking (4.50) kan in vergelijking (4.34/E1) ingevuld worden en dan ziet dat er zo uit:
Vervolgens is het een kwestie van haakjes wegwerken, waarna we maar liefst 64 termen hebben...
Daarna nemen we termen met gelijke dx
σdx
τ samen en tellen de α’s bij elkaar op.
De optellingen van de α’s geven we nieuwe namen: g.
Ik hoop dat iedereen er mee kan leven, maar die hele geitenbrij ga ik hier niet uitschrijven, want uiteindelijk
komen we toch echt wel weer hier uit:
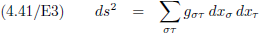 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
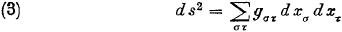
Zowel via de
inwendig-product-truc
van mij of via de benadering die Einstein kiest is duidelijk dat de g’s allemaal getallen
zijn
voor deze ene ds van de gebeurtenis G1 naar gebeurtenis G2.
Nu komt een belangrijke conclusie.
Het interval ds is invariant, iedere waarnemer meet hetzelfde interval ds, dat is een hele belangrijke basis om op
verder te bouwen.
En Einstein zegt het nog maar weer een keer: het interval ds is rechtstreeks meetbaar in de werkelijkheid met behulp
van meetlatten en klokken.
Het interval ds ligt dus vast zeg maar, en daarmee natuurlijk ook ds
2.
En die dx
σ en dx
τ kunnen iedere kant opwijzen en van punt tot punt verschillen.
De g
στ zijn daardoor functies van x en veranderlijk van punt tot punt.
Bovendien is het x-systeem (kleine letter “x”) het coördinatenstelsel dat we zelf kiezen en het X-systeem (grote
letter “X”) het ‘lokale’ coördinatenstelsel.
In vergelijking (4.41/E3) komen die grote X’en helemaal niet voor en de g’s zijn functies van de kleine x’en.
Dit laatste is essentieel en via mijn afleiding met de
inwendig-product-truc beter inzichtelijk
(vind ik), omdat ik daar het ‘lokale’ stelsel volledig buiten beschouwing laat.
Uit mijn afleiding is ook heel duidelijk dat de g-metriek
altijd symmetrisch is, omdat het
inwendig product commutatief is.
Oftewel g
στ = g
τσ (altijd), terwijl Einstein het doet voorkomen alsof
daar nog een keuzevrijheid in bestaat (“Die g
στ sind hierbij so zu wählen”, wählen = kiezen).
Dit is typisch zo’n moment dat ik denk: zie ik nou wat over het hoofd?
Ik heb speciaal hiervoor nog even de nodige literatuur geraadpleegd, maar de metrische tensor is toch echt
per definitie symmetrisch.
De speciale relativiteitstheorie komt uit dit alles voort indien er voor een eindig gebied (dus niet noodzakelijkerwijs
een
oneindig klein gebied) de g
στ zo te kiezen zijn dat ze de volgende constante waarden
aannemen:
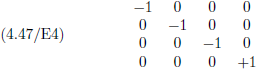 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
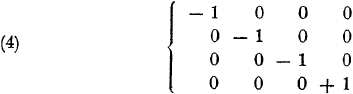
De som van de 1’en en −1’en op de
hoofddiagonaal noemt men de
signatuur
van de metrische tensor.
In dit geval is dat dus −2 of wat ook vaak als signatuuraanduiding wordt gebruikt is (−3, 1).
Je kunt ook spreken van het
spoor van de tensor.
Het spoor is de som van de componenten op de
hoofddiagonaal van een tensor en is altijd
een enkel getal.
De signatuur is eigenlijk een specifieke spooraanduiding van de metrische tensor.
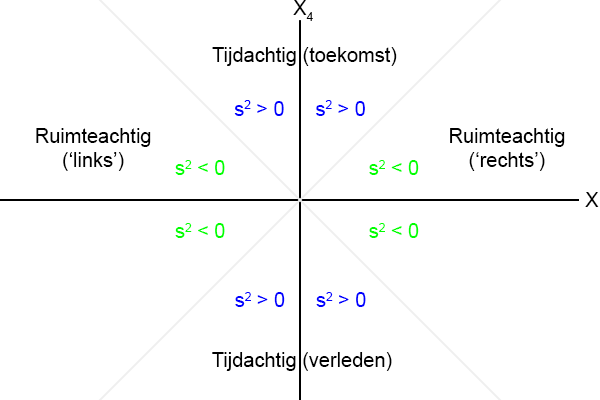
Tijdachtige intervallen (s
2 > 0) hebben aldus een
negatieve signatuur en ruimteachtige
intervallen (s
2 < 0) een
positieve signatuur zoals ik in onderstaand plaatje nogmaals heb
aangegeven.
Figuur 4.36
Indien de g
στ de waarden hebben volgens vergelijking (4.47), dan betekent dat dat een materieel punt (een
stukje materie zeg maar) met constante snelheid beweegt via een rechte lijn.
Wanneer we vervolgens overgaan naar een ander coördinatenstelsel, met andere ruimtetijdcoördinaten x
1,
x
2, x
3 en x
4, dan zullen de g
μν mogelijk geen constanten meer zijn
maar
ruimtetijdfuncties.
Even opletten hier: ineens wordt er niet meer over de indices στ gesproken maar over μν.
En in dit nieuwe stelsel zal dat stukje materie wellicht dan niet meer volgens een rechte lijn bewegen, maar een willekeurige
andere beweging volgen.
Wordt er wel volgens een rechte lijn bewogen dan werken er dus geen krachten in op het stukje materie, alles gaat
recht-toe-recht-aan, en een dergelijke ruimte noemen we een vlakke ruimte of ook wel
Minkowski-ruimte.
Wanneer er niet volgens een rechte lijn bewogen wordt dan zijn er krachten aan het werk die op dat stukje materie
inwerken (zie uitleg
paragraaf 2),
en volgens het
equivalentieprincipe
(zie ook uitleg
paragraaf 2)
kan dat ook uitgelegd worden als werking van de zwaartekracht.
Want, benadrukt Einstein, die inwerkende krachten zijn onafhankelijk van de aard van het stukje materie.
Het maakt niet uit of dat stukje materie uit lood bestaat of uit wol, en of het wel of niet elektrisch geladen is,
en of het wel of niet heet of koud is, enzovoort.
Zwaartekracht is de enige kracht die onafhankelijk werkt van al deze variabelen.
De zwaartekracht is gekoppeld aan de veranderlijkheid in de ruimtetijd van de g
στ.
De gστ beschrijven de metrische eigenschappen van de vierdimensionale ruimtetijd en tegelijkertijd het zwaartekrachtveld.
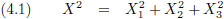
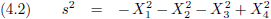
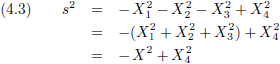
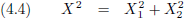

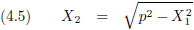
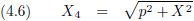

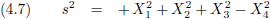
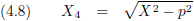







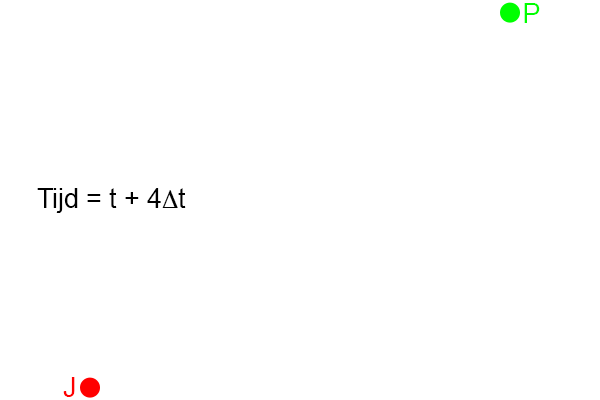



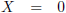
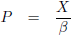
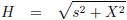
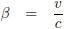
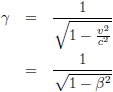
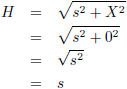
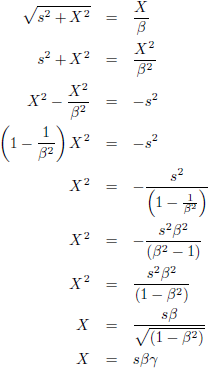
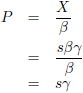

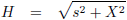
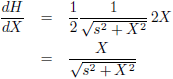
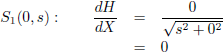
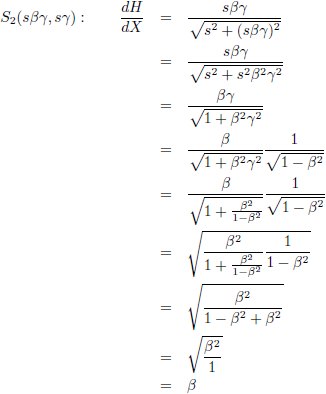
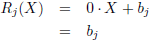
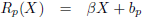
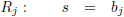
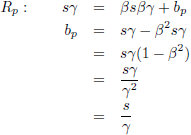

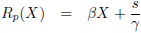

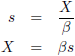









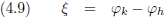
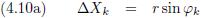
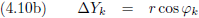
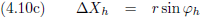
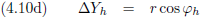
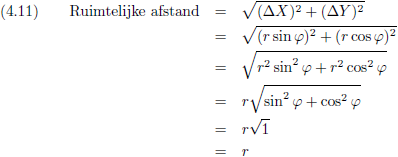
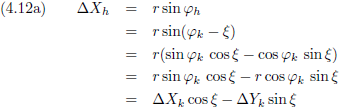
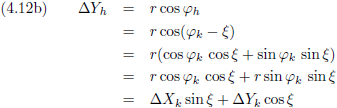

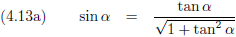
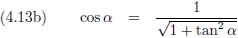
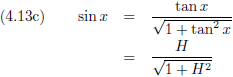
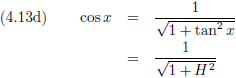
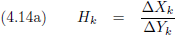
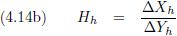
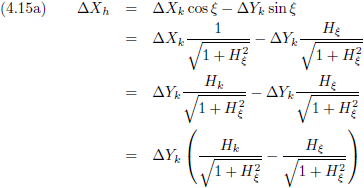
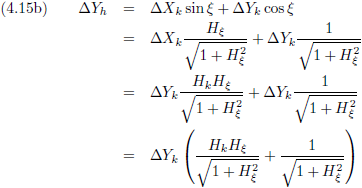
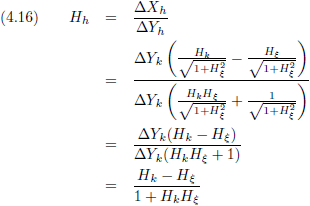

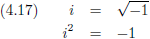
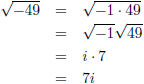
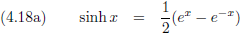
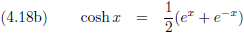
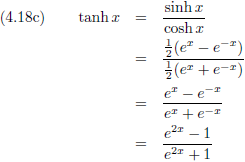
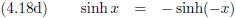
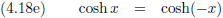
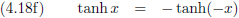
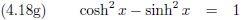
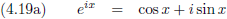
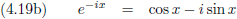
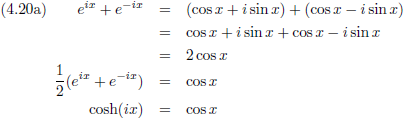
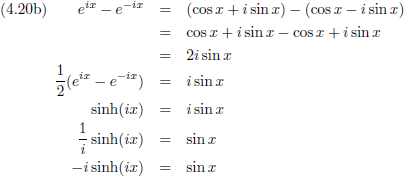
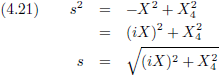
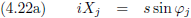
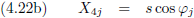
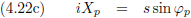
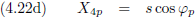
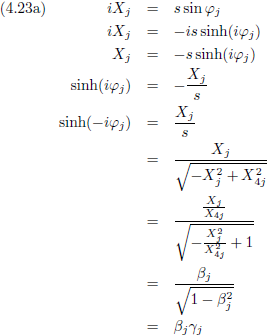
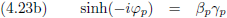
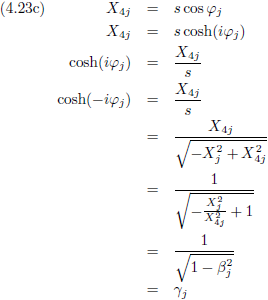
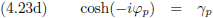
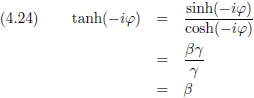
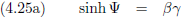
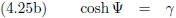
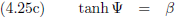
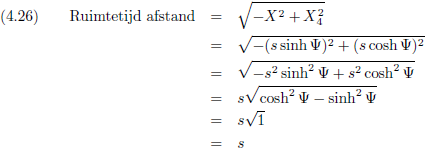
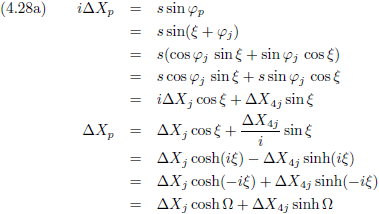
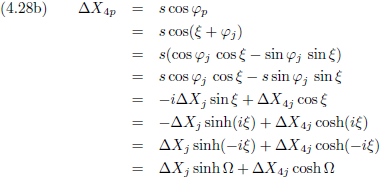
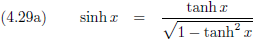
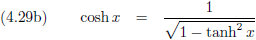
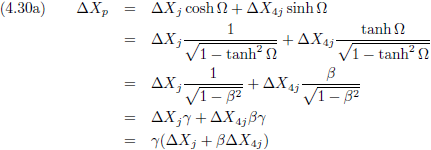
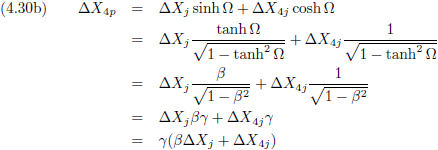
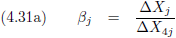
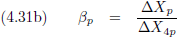
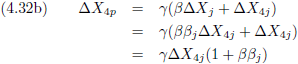
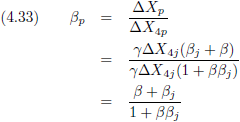
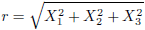
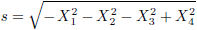
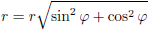
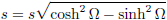
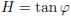
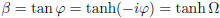
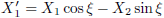
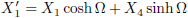
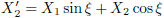
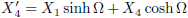
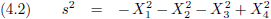
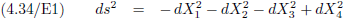
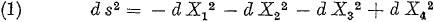











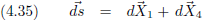
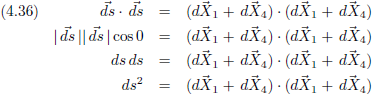
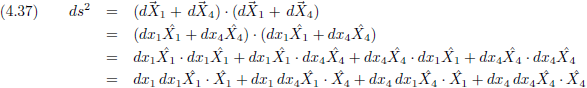
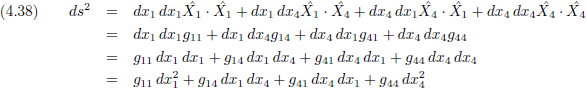
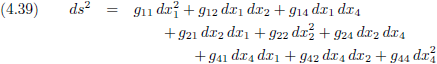
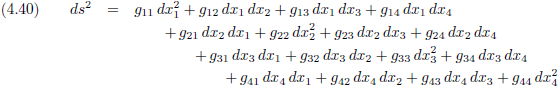
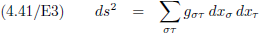
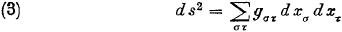
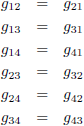
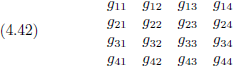
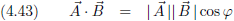
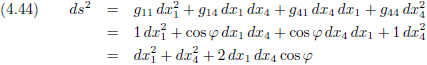
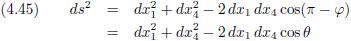

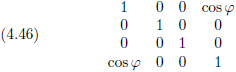
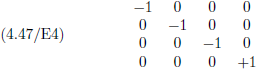
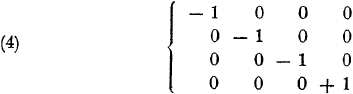
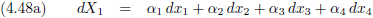
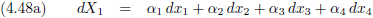
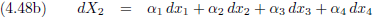
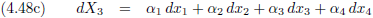
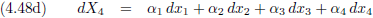
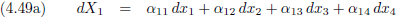
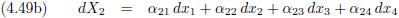
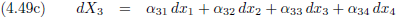

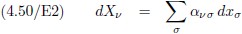

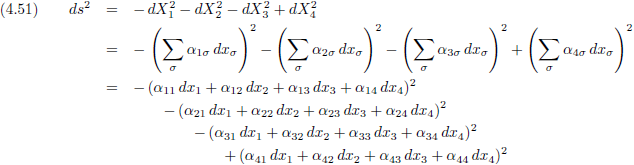
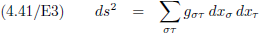
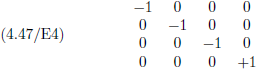
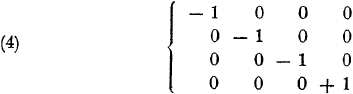












 Door naar de uitleg van de volgende paragraaf: inleiding hoofdstuk B
Door naar de uitleg van de volgende paragraaf: inleiding hoofdstuk B Terug naar de uitleg van de vorige paragraaf: paragraaf 3
Terug naar de uitleg van de vorige paragraaf: paragraaf 3 Naar de overzichtspagina van het artikel
Naar de overzichtspagina van het artikel Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van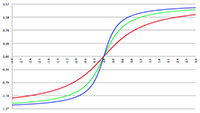 De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 74
Vectoren, vraagstuk 74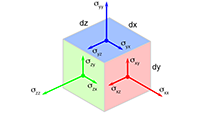 Vraagstukken tensoren
Vraagstukken tensoren De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van Het probleem van de gevangenen
Het probleem van de gevangenen Uitleg artikel E = mc2
Uitleg artikel E = mc2 Een raket, een tunnel en twee kanonnen
Een raket, een tunnel en twee kanonnen Klassiek als limietgeval van relativistisch
Klassiek als limietgeval van relativistisch Astronomie
Astronomie Elektriciteit en magnetisme
Elektriciteit en magnetisme Zou je als kind geïnspireerd zijn?
Zou je als kind geïnspireerd zijn? De illusie van verbinding (I)
De illusie van verbinding (I) Vertellingen
Vertellingen Babies, wiskunde en Geert Wilders
Babies, wiskunde en Geert Wilders Reacties op lezingen
Reacties op lezingen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen