Relativistische periheliumprecessie, 1e orde benadering
Bereken, uitgaande van de differentiaalvergelijking van een
geodetische lijn rondom een puntmassa, de
periheliumprecessie
van een planeet (in een
eerste orde benadering).
Dit is de differentiaalvergelijking van een
geodetische lijn rondom een puntmassa
(voor de afleiding zie
dit vraagstuk):
Waarbij voor u geldt:
Het slechte nieuws is: er is geen exacte oplossing bekend van deze differentiaalvergelijking.
Het goede nieuws is: in de wiskunde zijn we niet voor één gat te vangen.
Wanneer ik in vergelijking (1) de meest rechtse term weglaat dan blijft dit over:
De oplossing hiervan is de welbekende
eerste wet van Kepler
(planeten volgen elliptische banen):
De meest rechtse term van vergelijking (1) zal klein zijn, want anders was het al veel eerder opgevallen
dat de eerste wet van Kepler
niet precies klopt.
Sterker nog, dan zou Kepler nooit tot zijn eerste wet zijn gekomen, want hij heeft die immers afgeleid
uit waarnemingen.
Tycho Brahe had destijds de meest nauwkeurige waarneemgegevens en die stelden Kepler in staat om zijn
wetten op te stellen.
Let wel, die hele rechterterm, inclusief de u2, is klein, maar dat hoeft niet te gelden
(en dat geldt ook niet) voor het getal 3GM/c2 dat ervoor staat.
Ik ga daarom vergelijking (1) wat verbouwen.
Ik stel:
Waardoor (1) overgaat in:
Vervolgens stel ik:
Op deze manier weet ik zeker dat λ een klein getalletje is.
Vergelijking (6) wordt dan:
Vervolgens stel ik dat mijn oplossing eruit moet zien als volgt:
Ik besluit voor een eerste orde benadering te gaan:
En dit vul ik in in vergelijking (8):
Zoals gezegd ga ik voor een eerste orde benadering en daarom ga ik die termen met λ
2 en
λ
3 verwaarlozen:
Dit resultaat ga ik een beetje reorganiseren:
En vervolgens deel ik het op in twee vergelijkingen, termen zonder λ en termen met λ:
De oplossing van (14a) is simpel, dat is de klassieke Kepler-oplossing:
En deze oplossing vul ik in in vergelijking (14b):
Vergelijking (16) ga ik opdelen in drie vergelijkingen:
De oplossing van (17a) is simpel, dat is weer de klassieke Kepler-oplossing:
Voor de andere twee is het een beetje zoeken en aftasten (zoals meestal met differentiaalvergelijkingen),
maar de algemene oplossing van:
Is dit:
Bewijs:
En de algemene oplossing van:
Is dit:
Bewijs:
De oplossing van (17b) wordt daarmee:
En de oplossing van (17c) wordt:
De totale oplossing van u
1 is de som van (18), (25) en (26):
En de totale oplossing van u (zie vergelijking (10)) is de som van (15) en (27):
De afstand r is de reciproke hiervan:
Nu kunnen we terug naar de beginvraag van deze pagina: wat is de precessie van het
perihelium?
In het
perihelium
is r minimaal en dus de noemer van vergelijking (29) maximaal.
Ik neem die noemer daarom even apart onder de loep:
Voor het maximaal zijn van deze noemer spelen de constanten geen rol en die kunnen er dus uit:
Die term met λ cos φ is gemiddeld over een hele omloop van de planeet nul en draagt daarom ook niets bij.
En die term met cos
2 φ is gemiddeld over een hele omloop van de planeet constant en draagt daarom
op de lange duur ook niets bij.
Weg ermee:
En ik kan natuurlijk een factor e uitdelen:
Hetgeen ik ook kan schrijven als:
Omdat λφ heel klein is geldt bij zeer goede benadering:
Hiermee kan ik (34) schrijven als volgt:
Met behulp van de
som-/verschilformules
uit de
goniometrie wordt dit:
De
cosinus
is maximaal bij veelvouden van 2π:
Oftewel:
In de tabel met Taylor-reeksen vinden we:
Hiermee kan ik vergelijking (39) anders opschrijven:
Ik beperk mij weer tot de eerste orde term:
Hetgeen ons uiteindelijk brengt bij de precessie, de rechterterm van (42):
Met gebruikmaking van (7b) wordt dit:
De precessie per omloop is dan:
Wanneer ik dan tenslotte de
derde wet van Kepler,
die het verband geeft tussen omlooptijd en halve lange baanas, erin betrek:
Dan kom ik precies bij het resultaat zoals Einstein het iets meer dan honderd jaar geleden ook vond (maar dan wel op
een hele andere manier):
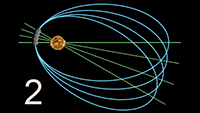
De planeetbanen blijken geen gesloten ellipsen te zijn, maar er zit een minimale draaiing in de baan zelf
waardoor de planeetbaan de vorm van een rozet aanneemt (sterk overdreven getekend op het plaatje hiernaast, want de
precessie is in werkelijkheid (veel) minder dan de diameter van de planeet).
De blauwe punten zijn de periheliumpassages
en die zijn het ijkpunt geworden voor deze relativistische precessie (terwijl je net zo goed over
apheliumprecessie kunt spreken of
over de precessie van ieder willekeurig ander punt van de planeetbaan, maar dat terzijde).
Het minieme verschil tussen ‘Newtonse zwaartekracht’ en de werkelijkheid werd in 1855 ontdekt door de Fransman
Urbain Le Verrier voor de planeet Mercurius.
Weliswaar is het verloop van de
periheliumprecessie
van Mercurius nog geen dertig kilometer per mercuriusjaar, en daardoor
nauwelijks waarneembaar, maar een mercuriusjaar duurt minder dan drie maanden op Aarde waardoor per aardejaar het verloop
al ruim honderd kilometer is (vier maal zoveel) en per eeuw ruim tienduizend kilometer (honderd maal zoveel).
Dit laatste viel ook in de negentiende eeuw al op, om te beginnen dus door Le Verrier.
Voor de planeet Mercurius berekende Le Verrier een afwijking van 38 boogseconden per eeuw en hij ging ervan uit dat een
nog onontdekte planeet tussen Mercurius en de Zon deze afwijking veroorzaakte.
Deze planeet kreeg alvast een naam, Le Verrier doopte de planeet Vulcanus, maar ondanks alle inspanningen werd de planeet
nooit gevonden.
































































 Door naar het volgende vraagstuk: relativistische periheliumprecessie, 2e orde benadering
Door naar het volgende vraagstuk: relativistische periheliumprecessie, 2e orde benadering Terug naar het vorige vraagstuk: stabiliteit van cirkelvormige banen om een centrale massa
Terug naar het vorige vraagstuk: stabiliteit van cirkelvormige banen om een centrale massa Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie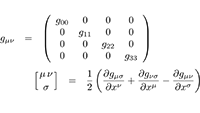 Christoffel-symbolen van de eerste soort bij een diagonale metriek
Christoffel-symbolen van de eerste soort bij een diagonale metriek De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 5
Vectoren, vraagstuk 5 Vectoren, vraagstuk 43
Vectoren, vraagstuk 43 Vectoren, vraagstuk 81
Vectoren, vraagstuk 81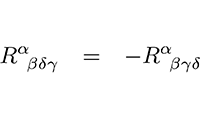 Anti-symmetrie in de Riemann-tensor
Anti-symmetrie in de Riemann-tensor De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van Matrices
Matrices Uitleg artikel algemene relativiteitstheorie: paragraaf 4
Uitleg artikel algemene relativiteitstheorie: paragraaf 4 Gelijktijdigheid
Gelijktijdigheid De maximale snelheid
De maximale snelheid De posities van de Lagrange-punten
De posities van de Lagrange-punten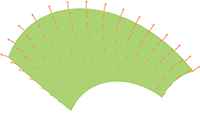 De potentialen van het elektromagnetische veld
De potentialen van het elektromagnetische veld De illusies die wij leven
De illusies die wij leven De illusie dat ik geen keus heb
De illusie dat ik geen keus heb Axiomahekken
Axiomahekken Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen