Optellen van snelheden zonder invariantie van de lichtsnelheid
Leid de vergelijking af voor het relativistisch optellen van twee snelheden zonder gebruik te maken van
de invariantie van de lichtsnelheid.
De lichtsnelheid is invariant en dat betekent dat licht door iedere waarnemer met dezelfde snelheid
wordt waargenomen.
Deze snelheid duiden we aan met c.
Vanuit dit gegeven is het vervolgens een redelijk simpel wiskundig pad dat naar de
Lorentz-transformaties leidt.
En van daaruit kun je vervolgens de vergelijking afleiden voor het
relativistisch optellen van snelheden.
Wat op z’n zachtst gezegd opmerkelijk is, is dat het afleiden van de vergelijking voor het
relativistisch optellen van snelheden ook te doen is
zonder gebruik te maken van de Lorentz-transformaties.
Newton zou de vergelijking al afgeleid kunnen hebben (of een andere slimmerik die voor Einstein leefde).
Maar goed, zo is het niet gelopen.
Pas nadat Einstein de speciale relativiteitstheorie voor het voetlicht had gebracht (in 1905) was het
Vladimir Ignatovski die vijf jaar later als eerste de
Lorentz-transformaties afleidde zonder lichtinvariantie.
In nagenoeg alle literatuur over relativiteitstheorie wordt dit bijzondere aspect volledig genegeerd.
Ik ga hier de vergelijking afleiden voor het
relativistisch optellen van snelheden zonder gebruik te
maken van andere natuurkunde (en dan bedoel ik met name het elektromagnetisme).
Ik begin met het maken van vier aannames:
- ruimte is homogeen (de ruimte ‘hier’ is niet anders dan de ruimte ‘daar’),
- tijd is homogeen (de tijd ‘nu’ is niet anders dan de tijd ‘straks’),
- ruimte is isotroop (de ruimte is in alle richtingen hetzelfde),
- transformaties zijn van dezelfde vorm als de inverse transformaties (het relativiteitsprincipe).
De eerste twee zijn alleen al noodzakelijk, omdat we anders geen natuurkunde kunnen bedrijven.
Want stel ik doe een experiment of een meting en de uitkomst zou afhankelijk zijn van het tijdstip en de
plaats van uitvoeren dan heeft het experiment of meting totaal geen zin.
Diezelfde combinatie van tijdstip en plaats komt immers nooit meer terug.
De andere twee aannames zijn het fundament onder het relativiteitsprincipe.
Kort door de bocht: zie ik jou naar rechts bewegen met een bepaalde snelheid dan zie jij mij naar links
bewegen met exact dezelfde snelheid.
Dan kunnen we nu ‘echt’ aan het werk.
Stel ik heb drie stelsels: S
1, S
2 en S
3.
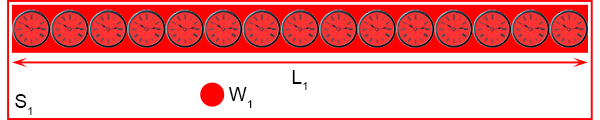
In het stelsel S
1 bevindt zich een waarnemer W
1 en een balk.
Deze waarnemer W
1 heeft zijn systeem volgezet met klokken die allemaal keurig gelijk lopen.
Verder heeft hij de lengte van de balk opgemeten en die heeft de lengte L
1.
Alles in dit systeem is in rust ten opzichte van hem, dus dat maakt het leven eenvoudig en hij heeft
zeeën van tijd om deze klussen te klaren.
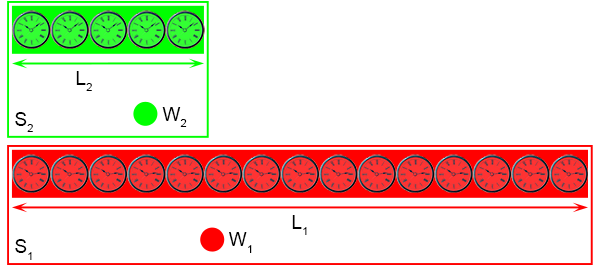
In het stelsel S
2 bevindt zich eveneens een waarnemer met een balk.
In dit systeem is de situatie niet anders, de waarnemer W
2 heeft zijn systeem ook volgezet met
klokken die allemaal keurig gelijk lopen.
Verder heeft hij ook de lengte van de balk opgemeten en die heeft de lengte L
2.
Alles in dit systeem is in rust ten opzichte van hem, dus dat maakt het leven wederom eenvoudig en hij heeft
eveneens zeeën van tijd om deze klussen te klaren.
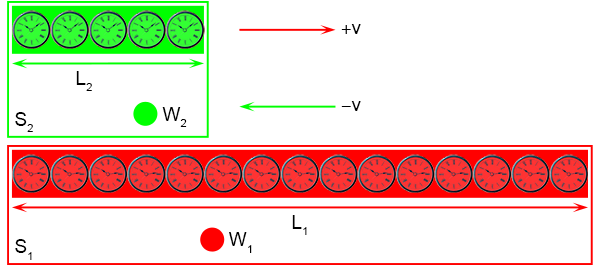
Beide stelsels bewegen ten opzichte van elkaar met een constante snelheid v.
W
1 ziet W
2 voorbijkomen met een snelheid +v en W
2 ziet W
1
voorbijkomen met een snelheid −v.
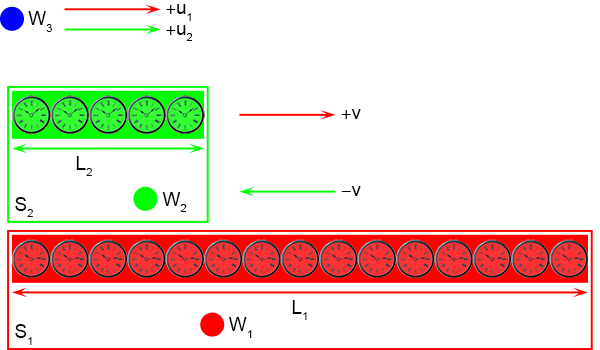
Er is nog een derde stelsel en daar bevindt zich de waarnemer W
3.
W
1 ziet W
3 voorbijkomen met een snelheid +u
1 en W
2 ziet W
3
voorbijkomen met een snelheid +u
2.
Op een bepaald moment vallen de linkerkanten van beide balken samen en dat gebeurt precies op het moment dat
W
3 daar passeert.
Dit noem ik gebeurtenis G
1.
Voor W
1 is dit op het tijdstip T
1a en voor W
2 op het tijstip T
2a.
Enige tijd later vallen de rechterkanten van beide balken samen en toevallig is W
3 weer ter plekke
om dat te zien gebeuren.
Dit noem ik gebeurtenis G
2.
Voor W
1 is dit op het tijdstip T
1b en voor W
2 op het tijstip T
2b.
Aan de snelheden waarmee ze elkaar onderling waarnemen verandert uiteraard niets.
Het tijdsverschil tussen beide gebeurtenissen is voor W
1 respectievelijk W
2:
De lengte van de rode balk is voor W
1 respectievelijk W
2:
De lengte van de groene balk is voor W
1 respectievelijk W
2:
De snelheid van W
3 is voor W
1 respectievelijk W
2:
De lengte van de rode balk zoals die door beide waarnemers wordt waargenomen heeft een bepaalde
onbekende verhouding (in de teller staat de waarneming van de bewegende waarnemer en in de noemer
staat de waarneming van de stilstaande waarnemer, maar dat had ik natuurlijk net zo goed kunnen
verwisselen):
En het relativiteitsprincipe vereist dat dit dan ook moet gelden voor de groene balk:
De verhouding volgens vergelijking (5a)
moet gelijk zijn aan de verhouding volgens (5b), want
anders ligt het relativiteitsprincipe in duigen.
Uit de vergelijkingen (5) volgt:
Vervolgens deel ik (6b) door (6a):
Dit resultaat stop ik in vergelijking (4a):
En de vergelijking (6b) stop ik op twee verschillende manieren in de vergelijking (4b) (eerst om L
2 te
elimineren en daarna om T
2 te elimineren):
En deze twee vergelijkingen gaan tenslotte in vergelijking (8):
De factor α mag niet afhankelijk zijn van ruimte of tijd, want dan schenden we één of meer van onze basisaannames.
Oftewel, α kan alleen afhangen van de relatieve snelheid tussen twee waarnemers:
En indien die relatieve snelheid gelijk is aan nul dan moet α gelijk aan één zijn.
Een blik op de vergelijkingen (5) maakt dat duidelijk, oftewel a
0 = 1:
Tenslotte moet α een even functie zijn van de relatieve snelheid (lees: een functie zijn van het kwadraat van
die snelheid) om fysisch onmogelijke tekenwisselingen te voorkomen wanneer de relatieve snelheid omkeert van richting.
Dit betekent dat alle oneven termen nul moeten zijn:
Omdat α een functie is van v
2, dan is α
2 dat natuurlijk ook:
En (1 − α
2) wordt dan:
En dit stop ik in vergelijking (10):
De snelheden u
2 en v moet ik probleemloos kunnen verwisselen voor hetzelfde resultaat, want anders ligt
het relativiteitsprincipe weer aan gruzelementen:
Het moge duidelijk zijn dat de vergelijkingen (16a) en (16b) verschillende uitkomsten op gaan leveren.
Tenzij, en dat is de enige oplossing, alle coëfficiënten b
n nul zijn behalve b
1.
De vergelijkingen (16) worden dan:
Zo is alles weer met elkaar ‘in balans’.
Ik stel:
Zodat ik uiteindelijk kom tot dit resultaat (ik schrijf het even op voor twee willekeurige snelheden):
Een spectaculair resultaat!
Terwijl ‘iedereen’ relativiteitstheorie direct associeert met de lichtsnelheid en met elektromagnetisme
blijkt dat je relativistische principes ook kunt afleiden gebaseerd op een handvol logische aannames.
Toch wil ik even bekennen dat ik onderweg vals heb gespeeld.
Wat is er aan de hand?
Ik vertelde aan het begin van deze afleiding dat waarnemer W
1 ervoor had gezorgd dat alle rode
klokken keurig gelijk lopen, en dat waarnemer W
2 ervoor had gezorgd dat alle groene klokken keurig
gelijk lopen.
Maar hoe hebben ze dat gedaan?
Het simpele antwoord is: dat kunnen ze niet!
Voor het synchroniseren van klokken heb je namelijk een signaal nodig met een invariante snelheid en ze zijn
juist bezig om te ontdekken dat er überhaupt zoiets als een invariante snelheid bestaat.
Met andere woorden: er zit een cirkelredenering in dit verhaal.
Is er nog iets te redden van deze pagina?
Jazeker, ik heb gewoon meer waarnemers nodig.
We zetten alle klokken overboord en huren meer waarnemers in.
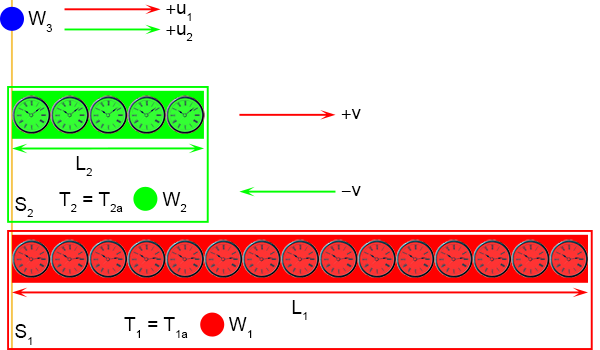
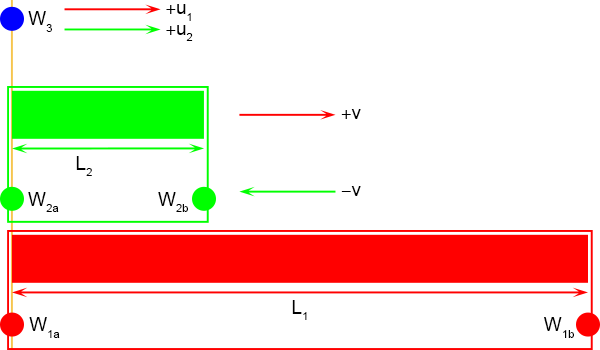
Dit wordt dan de situatie tijdens gebeurtenis G
1.
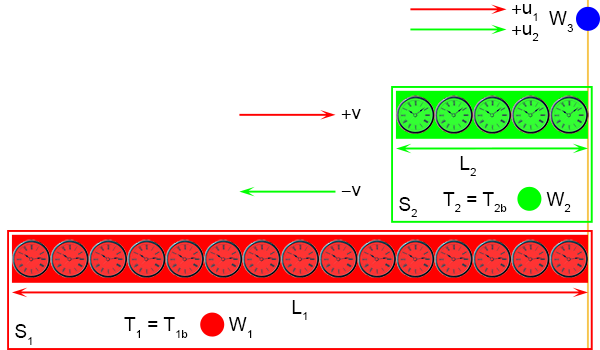
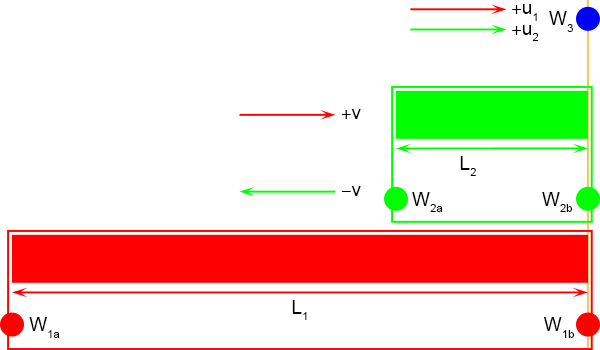
En dit wordt de situatie tijdens gebeurtenis G
2.
Het belangrijkste is dat ze waarnemen dat bij G
1 de linkerkanten samenvallen en bij G
2
de rechterkanten.
En wat de waarnemers in hun eigen stelsel (het stelsel waarin ze in rust zijn) aan afstanden en tijdsverschillen
meten is niet relevant, die vallen uiteindelijk toch uit de vergelijkingen.
Dus
wat ze meten is niet van belang,
als ze maar meten.
Klopt, ik had ook gelijk met vijf waarnemers kunnen beginnen, maar dit leek me handiger.
Tegenwoordig weten we dat voor K geldt:
Om invulling te geven aan de constante K dan heb je uiteindelijk wel het elektromagnetisme nodig, maar dat doet
geen enkele afbreuk aan het feit dat je de basisprincipes van de relativiteitstheorie boven water kunt krijgen
zonder gebruik te maken van andere natuurkunde.
Dat zag zelfs Einstein niet aankomen!
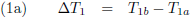
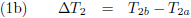
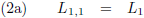
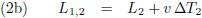
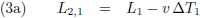
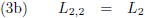
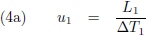
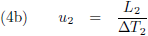
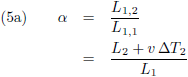
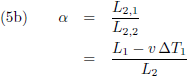
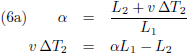
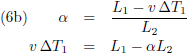
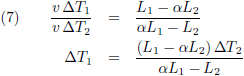
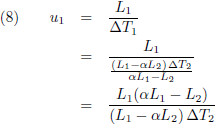
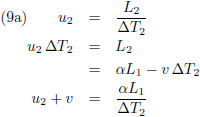
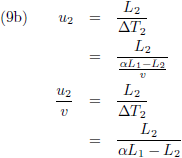
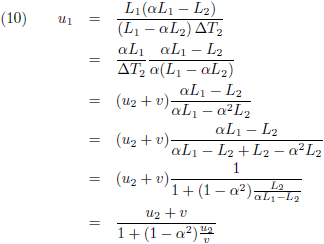
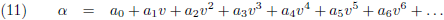
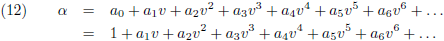
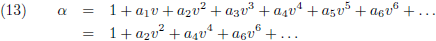
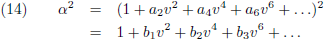
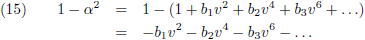
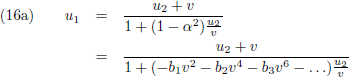
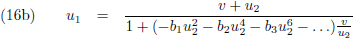
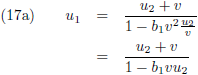
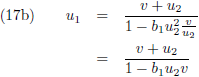
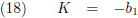
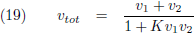
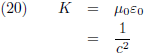




 Door naar het volgende vraagstuk: de maximale snelheid
Door naar het volgende vraagstuk: de maximale snelheid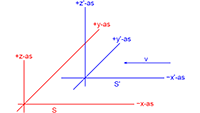 Terug naar het vorige vraagstuk: Lorentz-transformaties zonder invariantie van de lichtsnelheid
Terug naar het vorige vraagstuk: Lorentz-transformaties zonder invariantie van de lichtsnelheid Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 34
Vectoren, vraagstuk 34 Vectoren, vraagstuk 72
Vectoren, vraagstuk 72 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van De schipbreukeling op het eiland
De schipbreukeling op het eiland Relativiteitstheorie rekenkundig, hoofdstuk 8: rekenvoorbeelden
Relativiteitstheorie rekenkundig, hoofdstuk 8: rekenvoorbeelden De ontsnappingssnelheid
De ontsnappingssnelheid Het relativistische impulsmoment van een holle bol
Het relativistische impulsmoment van een holle bol Astronomie
Astronomie Elektriciteit en magnetisme
Elektriciteit en magnetisme Terugkijkend vanaf je sterfbed, wat ga je NU doen?
Terugkijkend vanaf je sterfbed, wat ga je NU doen? De illusie van versheid
De illusie van versheid Vertellingen
Vertellingen Trump en de schoonheid van de werkelijkheid
Trump en de schoonheid van de werkelijkheid Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat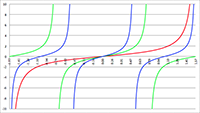 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)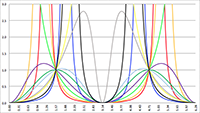 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2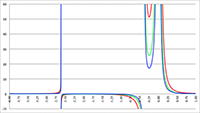 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen