De Schwarzschild-metriek in isotrope coördinaten
Schrijf de Schwarzschild-metriek om van bolcoördinaten naar isotrope coördinaten.
De Schwarzschild-metriek is de metrische tensor die hoort bij de
Schwarzschild-oplossing:
Het interval ziet er dan als volgt uit:
Een ruimtelijk afstandje ziet er in Cartesische coördinaten op deze manier uit, dat is simpelweg de
Stelling van Pythagoras:
En in bolcoördinaten ziet een ruimtelijk afstandje er zo uit:
Het liefst willen we het interval dan ook in de volgende vorm schrijven, waarbij het soort coördinaten op een bepaalde
manier verstopt zit in dσ:
Wanneer ik de bovenstaande vergelijkingen overzie dan kom ik al snel tot de conclusie dat Ω gelijk aan één moet
zijn en ben ik weer terug bij af (terwijl ik nog maar net uit de startblokken ben).
Kortom, ik heb een extra vrijheidsgraad nodig.
Daarom introduceer ik een nieuwe radiële coördinaat ρ die een functie is van de oude radiële coördinaat r: ρ (r).
Wanneer ik σ uitschrijf in de oude radiële coördinaat r (vergelijking (4)) dan geldt Ω = 1, maar wanneer ik
σ uitschrijf in de nieuwe radiële coördinaat ρ dan ontstaat er speelruimte:
Door de vergelijkingen (2) en (6) met elkaar te vergelijkingen kom ik tot de conclusie dat altijd moet gelden:
Indien de vergelijkingen (7) op enig moment niet gelden dan ligt uiteraard het interval in duigen.
Uit vergelijking (7b) volgt:
Hiermee wordt vergelijking (7a):
Ik ga beide zijden
integreren, de oplossing van de
integraal
in het linkerlid zoek ik op in de
tabel met integralen
en de oplossing van de
integraal
in het rechterlid zoek ik ook op in de
tabel met integralen:
Wat ga ik doen met de
integratieconstante C?
Het is wel fijn indien voor grote waarden van r en ρ, daar waar de ruimte vlak is, beide coördinaten naadloos
in elkaar overgaan:
Hieruit volgt voor C:
Aldus wordt vergelijking (10):
Om dit op te lossen (want ik wil r weten als functie van ρ) doe ik eerst even het volgende tussenstapje:
Oftewel:
Vervolgens tel ik de vergelijkingen (13) en (15) bij elkaar op:
Hiermee wordt vergelijking (8):
En met behulp van vergelijking (16) ga ik g
00 omschrijven:
De vergelijkingen (17) en (18) substitueer ik tenslotte in vergelijking (5) om tot het eindantwoord te komen:
Voor de overzichtelijkheid kan ik eventueel nog stellen:
Zo krijgt vergelijking (19) deze compacte vorm:
Ik stel:
Dat brengt ons bij dit overzicht:

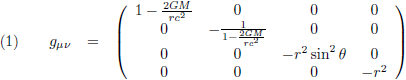

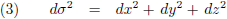
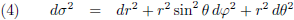
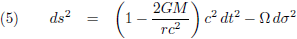
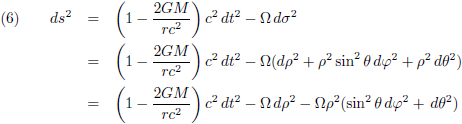
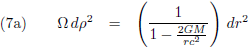
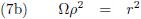
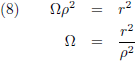
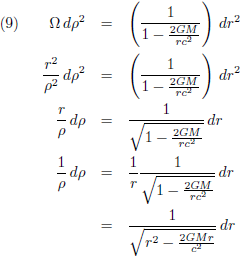
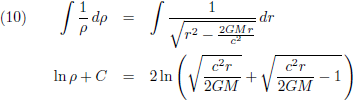
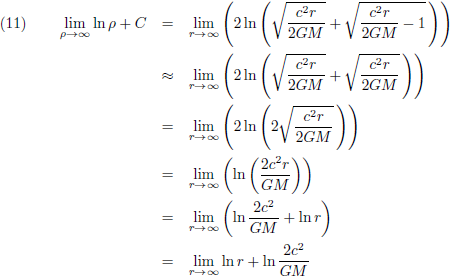
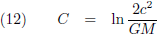
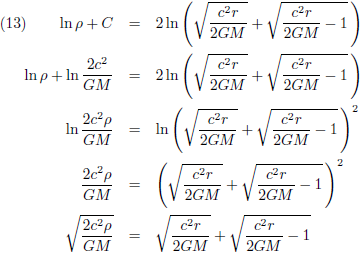
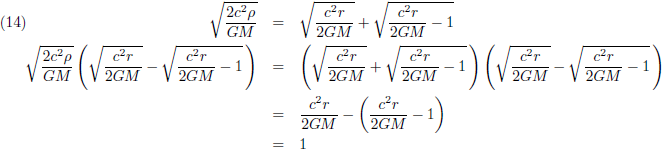
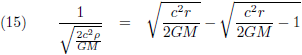
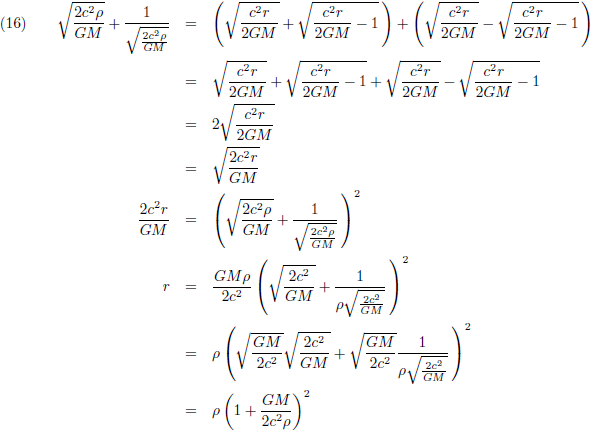
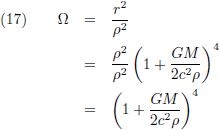
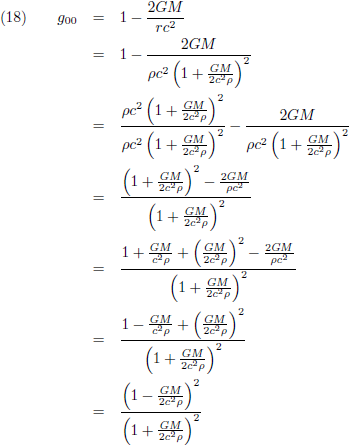
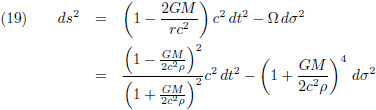
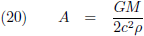
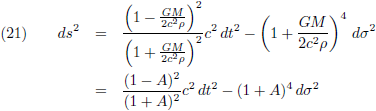
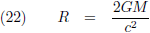
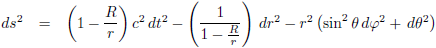
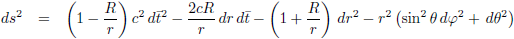
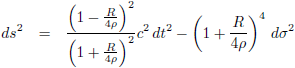


 Door naar het volgende vraagstuk: de Schwarzschild-oplossing van de algemene relativiteitstheorie
Door naar het volgende vraagstuk: de Schwarzschild-oplossing van de algemene relativiteitstheorie Terug naar het vorige vraagstuk: kinetische energie
Terug naar het vorige vraagstuk: kinetische energie Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie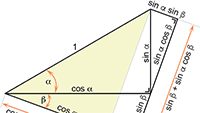 Goniometrie in het platte vlak
Goniometrie in het platte vlak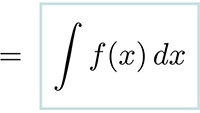 Integreren
Integreren De integraal van
De integraal van De integraal van
De integraal van Eddington-Finkelstein-coördinaten
Eddington-Finkelstein-coördinaten Christoffel-symbolen van de Schwarzschild-metriek
Christoffel-symbolen van de Schwarzschild-metriek De Ricci-tensor van de Schwarzschild-metriek
De Ricci-tensor van de Schwarzschild-metriek De Ricci-scalar van de Schwarzschild-metriek
De Ricci-scalar van de Schwarzschild-metriek Een analogie van het onzekerheidsprincipe van Heisenberg
Een analogie van het onzekerheidsprincipe van Heisenberg Wat doe je wanneer je uitstelgedrag vertoont?
Wat doe je wanneer je uitstelgedrag vertoont? De illusie van doen
De illusie van doen De reis naar de werkelijkheid van Lucia Prinsen
De reis naar de werkelijkheid van Lucia Prinsen De Natuur spreekt: Mountain/Berg
De Natuur spreekt: Mountain/Berg De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 57
Vectoren, vraagstuk 57 Vectoren, vraagstuk 95
Vectoren, vraagstuk 95 Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat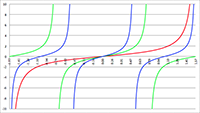 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)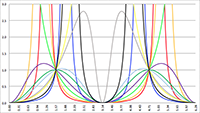 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2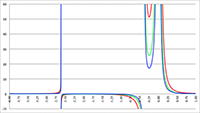 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen