De wetten van Kepler met niet-verwaarloosbare secundaire massa
Leid de drie wetten van Kepler af, waarbij de secundaire massa niet verwaarloosbaar is ten opzichte van de primaire massa.
De ontdekking dat de planeetbanen niet perfect cirkelvormig zijn maar elliptisch (ovaal) staat op naam van de Duitser Johannes Kepler.
Hij heeft ons drie wetten nagelaten volgens welke de planeten bewegen in hun baan om de Zon en die drie wetten gaan we hier afleiden.
Om te beginnen vormen we een coördinatenstelsel x-y-z waarvan de assen loodrecht op elkaar staan.
De oorsprong van dit stelsel valt samen met het zwaartepunt, zeg maar het middelpunt, van de Zon.
De massa van de Zon is m
z.
Op een afstand r van de oorsprong bevindt zich een planeet met massa m
p die in een baan om de Zon draait.
Deze planeet bevindt zich op coördinaten (x, y, z).
Er geldt:
De zwaartekracht die de planeet en de Zon op elkaar uitoefenen is volgens de zwaartekrachtwet van Newton (en opgesplitst in de x, y en z richting):
Door al dit getrek aan de Zon beweegt de Zon uiteraard, maar niet binnen het x-y-z-stelsel want de oorsprong van dit stelsel hebben we immers
in het zwaartepunt van de Zon neergelegd.
Vervolgens stellen we ons voor dat er zich ergens een ‘vast punt’ in de ruimte bevindt en dat punt bevindt zich in de oorsprong van het
coördinatenstelsel ξ-η-ζ.
Ten opzichte van het ξ-η-ζ-stelsel beweegt de Zon natuurlijk wel, en wel onder invloed van het getrek van de planeet zoals we
hierboven beschreven hebben:
Door de vergelijkingen (2) en (3) te combineren ontstaat:
De vergelijkingen (2) beschrijven de zwaartekracht die de planeet en de Zon op elkaar uitoefenen.
Oftewel, de planeet trekt aan de Zon maar de Zon trekt net zo hard aan de planeet.
In lijn met de vergelijkingen (4) kan ik als bewegingsvergelijkingen voor de planeet opschrijven (met een minteken voor het rechterlid, want
de planeet wordt richting de oorsprong, de Zon, getrokken):
Vanuit het ξ-η-ζ-stelsel bezien wordt dit:
Voor de
tweede afgeleiden
van de ξ-η-ζ-coördinaten kan ik, met behulp van de vergelijkingen (4), ook schrijven:
Door nu nog te stellen dat:
Zo komen we tot deze set vergelijkingen:
Door de vergelijking (9a) met y te vermenigvuldigen en (9b) met x, en vervolgens de resultaten van elkaar af te trekken krijgen we dit:
Ditzelfde ga ik ook doen door (9a) met z te vermenigvuldigen en (9c) met x, en (9b) met z te vermenigvuldigen en (9c) met y:
De vergelijkingen (10) ga ik
integreren:
Hierin zijn de c’s
integratieconstanten.
De vergelijkingen (11) ga ik vermenigvuldigen met respectievelijk z, −y en x, en ik tel ze alledrie bij elkaar op:
Dit is de vergelijking van een plat vlak, dus de planeet beweegt in een plat vlak en de Zon bevindt zich in datzelfde vlak (in de oorsprong).
Dit resultaat gaan we zometeen gebruiken.
Nog even dit tussendoortje.
Voor r
2 geldt:
Hieruit volgt door te
differentiëren:
Hier ga ik gebruik van maken bij het volgende.
Ik ga de vergelijkingen (9) vermenigvuldigen met respectievelijk 2dx, 2dy en 2dz, en bij elkaar optellen:
Vergelijking (15) ga ik vervolgens
integreren:
Dit resultaat parkeren we even.
Nu ga ik de vergelijkingen (11)
kwadrateren en bij elkaar optellen:
Ik stel:
Waarmee vergelijking (17) tenslotte wordt:
Indien de planeet een infinitesimaal stukje aflegt van zijn baan, dan geldt er voor dat stukje baanlengte
in Cartesische coördinaten (gewone x-y-z-coördinaten):
Dat is simpelweg de
stelling van Pythagoras
toepassen.
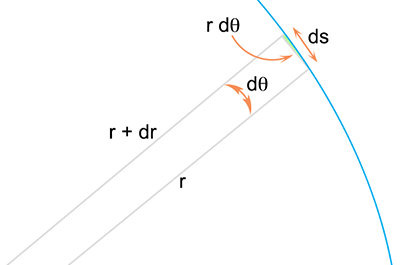
Figuur 1
Maar in poolcoördinaten ligt het iets ingewikkelder:
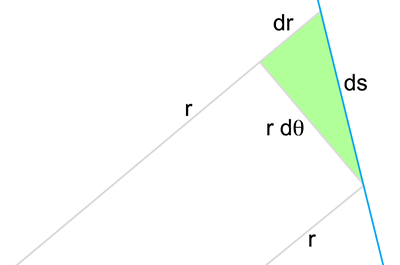
Figuur 2
Laat ik even inzoomen:
De infinitesimale verandering van r is dr, en loodrecht daarop staat r dθ.
Het stukje baanlengte in poolcoördinaten wordt dan:
Uit (20) en (21) volgt:
Dit vul ik in in (19):
Nu ga ik vergelijking (16) iets anders opschrijven:
En vergelijking (17) ook:
Door (24) en (25) te combineren krijg ik een uitdrukking voor dt:
En die vul ik in in (23):
Door dit iets anders op te schrijven heb ik in één klap de
afgeleide van r (naar θ):
En door (28) nul te stellen vind ik de extreme waarden van r:
De oplossing r = 0 is die waarbij beide hemellichamen op ramkoers liggen en waarbij ze uiteindelijk ook op elkaar botsen.
Maar het zijn natuurlijk de andere oplossingen die ons interesseren.
Ik stel:
Waarmee ik (29) als volgt kan schrijven:
Met deze kennis ga ik vergelijking (27) omschrijven:
Vervolgens ga ik
integreren:
Hier heb ik de vergelijking van een ellips!
De
integratieconstante
θ
0 is de hoek van waaraf θ wordt bepaald en die stel ik voor het gemak gelijk aan nul.
Vergelijking (34) kan ik tenslotte schrijven als:
Hierin is e de
numerieke excentriciteit, of kortweg
excentriciteit, van de ellips:
Met a als de halve lange as, b als de halve korte as en ε als de
lineaire excentriciteit van de ellips.
Voor de teller van (35) kan ik dus ook schrijven:
Ik schrijf nu (31) even iets anders op:
En vervolgens ga ik verder met vergelijking (26) en ik vul hier de waarden van de
integratieconstanten
in volgens (30) en (38), en ik maak ook gebruik van (8):
Bovenstaande vergelijking ga ik
integreren
waarbij ik als
integratiegrenzen
r = a (1 − e) en r = a (1 + e) neem, oftewel de punten van
kleinste afstand (het
perihelium)
en grootste afstand (het
aphelium) tot de Zon.
De tijdsduur hiervan (om van
perihelium
tot
aphelium te komen)
is uiteraard de helft van de totale omlooptijd T:
Voor twee planeten, p
1 en p
2 verhouden zich de
kwadraten van hun omlooptijden aldus:
Indien we de massa’s van de planeten verwaarlozen ten opzichte van de massa van de Zon dan verhouden de
kwadraten van hun omlooptijden zich
als de derde
machten van hun lange baanassen.
En indien we de planeetmassa’s niet kunnen verwaarlozen dan is het ongeveer de
derde
macht.
Tenslotte ga ik nog met vergelijking (23) aan de gang.
Ik vul daar de waarde van C in volgens (38) en de waarde van k volgens (8):
Het linkerlid is een infinitesimaal oppervlakje dO (de oppervlakte van een gelijkbenige driehoek is halve basis maal hoogte, zie ook figuur 1) van
de ellips en het rechterlid is de tijd voorafgegaan door een aantal constanten.
Door dit te gaan
integreren
tussens willekeurige
grenzen volgt hieruit:
Na al dit gereken hebben we alle ingrediënten bij elkaar om de wetten van Kepler op een rijtje te zetten.
De
eerste wet van Kepler zegt dat alle planeten in elliptische banen om de Zon bewegen, waarbij de Zon niet in het middelpunt van de
ellips staat maar in één van de
brandpunten.
Dit volgt uit vergelijking (35):
Met (32) heb ik het
aphelium
en het
perihelium berekend:
Merk op dat de som van beide gelijk is aan 2a, zijnde de lange as van de ellips.
De
tweede wet van Kepler zegt dat een planeet in gelijke tijdsintervallen gelijke oppervlakten bestrijkt, waarbij een oppervlakte gevormd
wordt door de taartpunt met de Zon aan de punt en de planeetbaan als de rand van de taart.
Deze wet zit verborgen in (43):
Deze wet is bekend onder de naam
perkenwet.
De
derde wet van Kepler zegt dat het
kwadraat
van de omlooptijd van een planeet evenredig is met de
derde
macht van de halve lange as
van de baan.
Dit is zichtbaar middels vergelijking (41):
Ik zet ze even netjes op een rijtje, de drie wetten van Kepler:
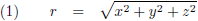
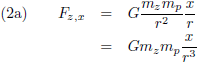
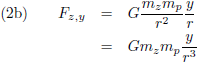
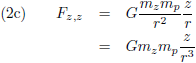
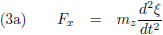
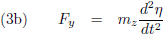
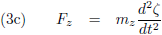
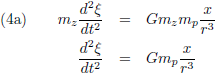
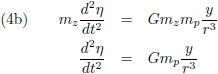
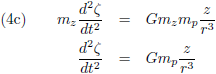
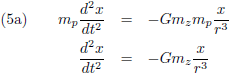
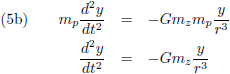
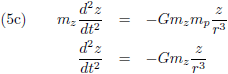
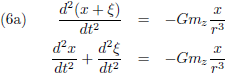
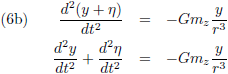
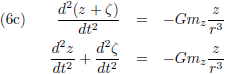
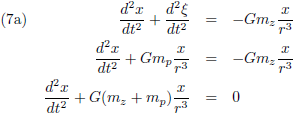
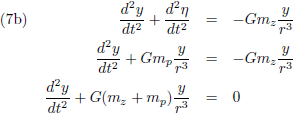
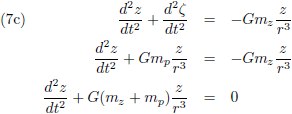
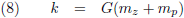
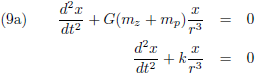
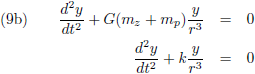
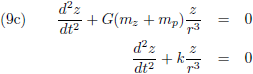
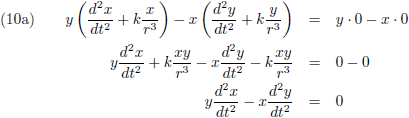
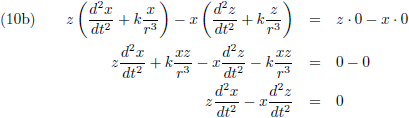
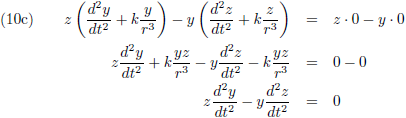
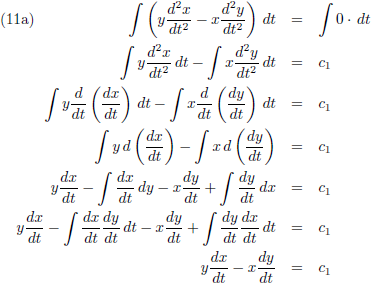
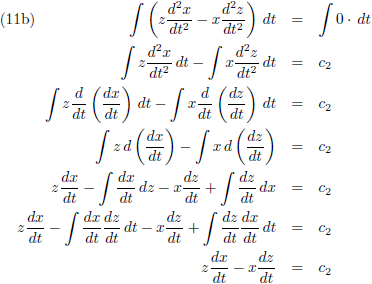
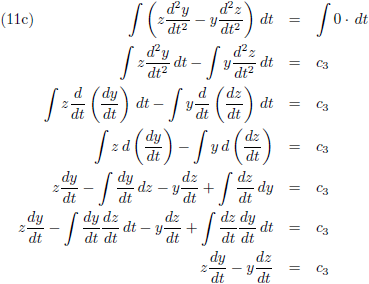
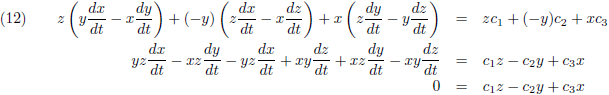

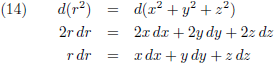
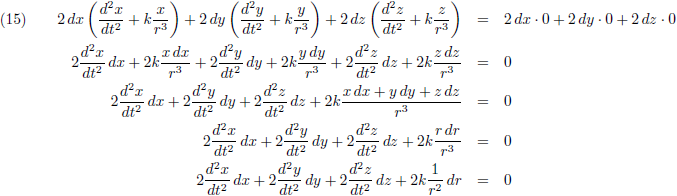
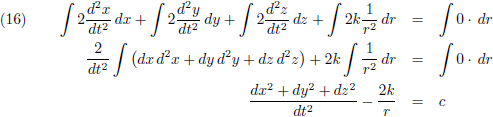
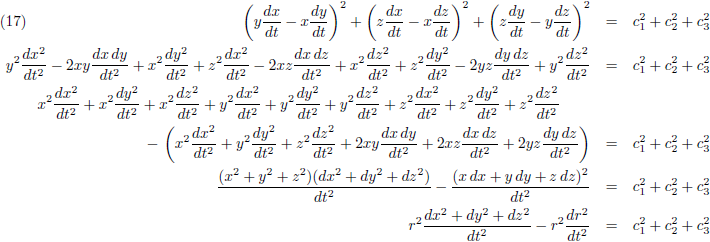
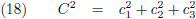
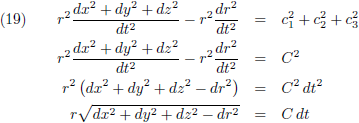
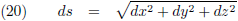


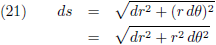
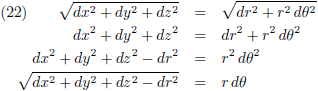
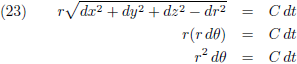
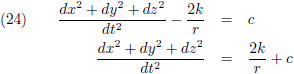
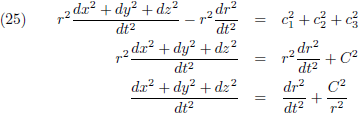
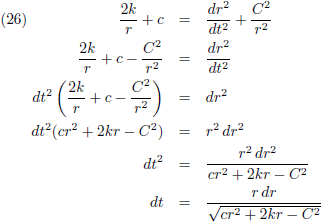
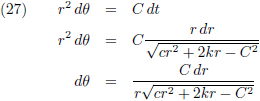
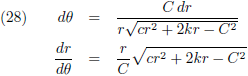
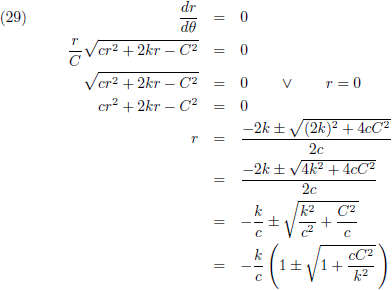
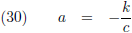
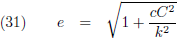
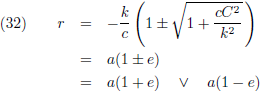
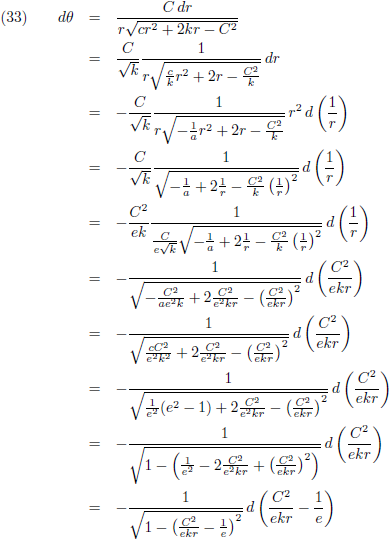
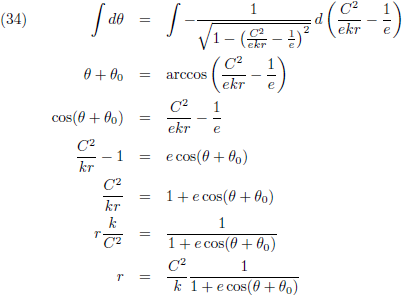
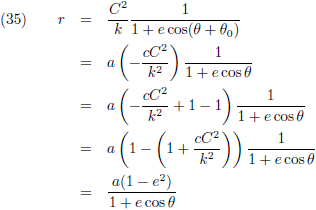
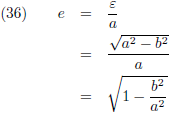
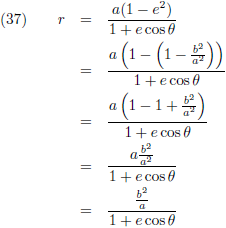
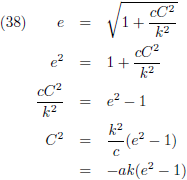
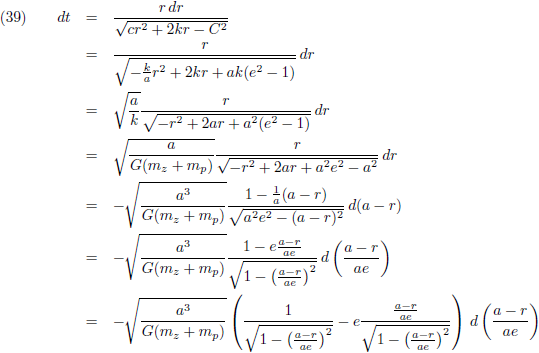
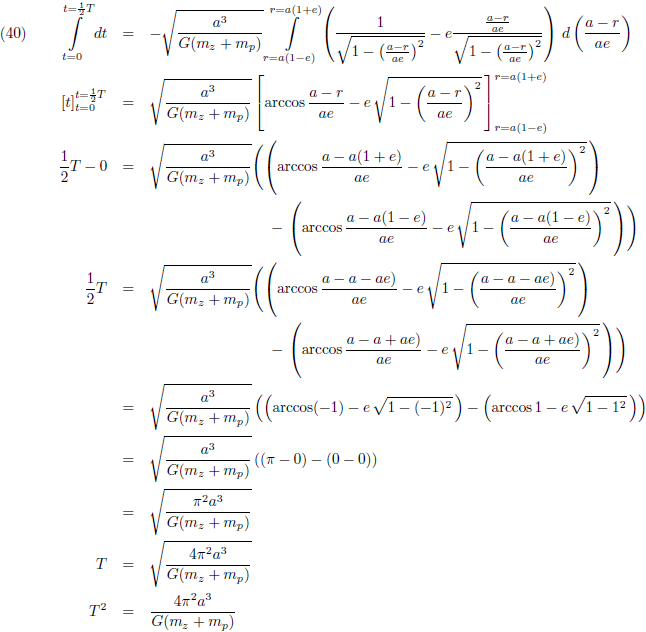
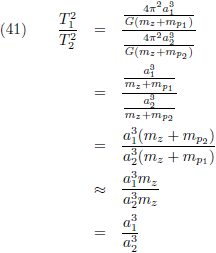
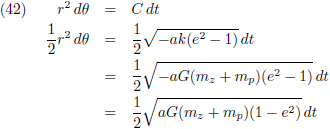
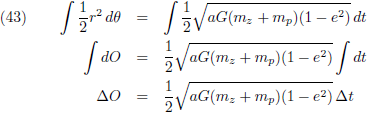
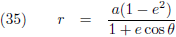
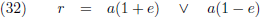
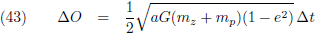
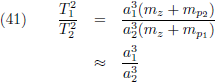



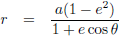
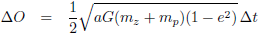
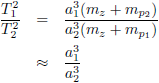
 Door naar het volgende vraagstuk: klassieke periheliumprecessie
Door naar het volgende vraagstuk: klassieke periheliumprecessie Terug naar het vorige vraagstuk: de wetten van Kepler met verwaarloosbare secundaire massa
Terug naar het vorige vraagstuk: de wetten van Kepler met verwaarloosbare secundaire massa Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina astronomie
Naar de overzichtspagina astronomie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 23
Vectoren, vraagstuk 23 Vectoren, vraagstuk 61
Vectoren, vraagstuk 61 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 6: voelen
Relativiteitstheorie basic, hoofdstuk 6: voelen Uitleg artikel algemene relativiteitstheorie: paragraaf 20
Uitleg artikel algemene relativiteitstheorie: paragraaf 20 Het equivalentieprincipe
Het equivalentieprincipe De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt Kwantummechanica
Kwantummechanica Is er voldoende zonne-energie voor de mensheid?
Is er voldoende zonne-energie voor de mensheid? De illusie van de temperatuur
De illusie van de temperatuur De reis naar de werkelijkheid van Steve Jobs
De reis naar de werkelijkheid van Steve Jobs De Afghanen komen
De Afghanen komen De Natuur spreekt: The Redwood/De Reuzenbomen
De Natuur spreekt: The Redwood/De Reuzenbomen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen