De snelheid van een baksteen die in een zwart gat valt
Wanneer ik vanaf grote afstand een baksteen in een niet-roterend zwart gat laat vallen, wat is dan de snelheid
van de baksteen op het moment dat die de horizon passeert bezien vanuit mij?
Ik ben diegene die de baksteen laat vallen en ik bevind mij op grote afstand van het
zwarte gat.
Oftewel, ik ben een verre stationaire waarnemer [Engels: distant observer of Schwarzschild observer
of bookkeeping observer of kortweg bookkeeper].
In dit vraagstuk heb ik de differentiaalvergelijkingen afgeleid van een geodetische lijn rondom een niet-roterende puntmassa. Een baksteen die ik loslaat in de buurt van een zwart gat beweegt onmiskenbaar geodetisch (de baksteen heeft geen aandrijvingsmechanisme, hij is in vrije val). Daarom neem ik wat vergelijkingen over van die pagina, om precies te zijn de vergelijkingen (13), (15) en (21):
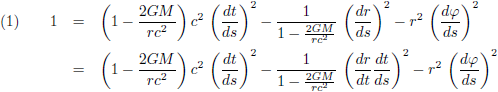
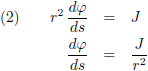
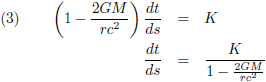
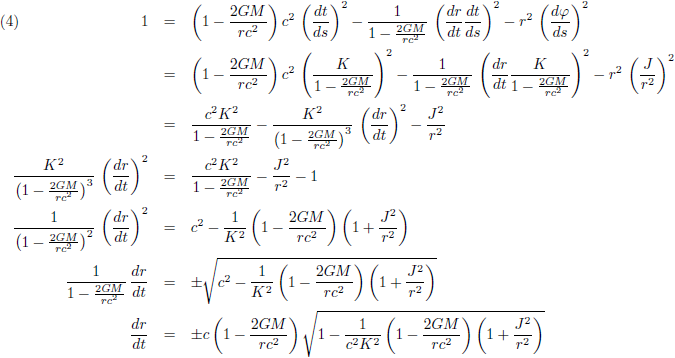
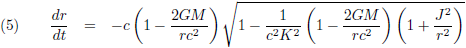
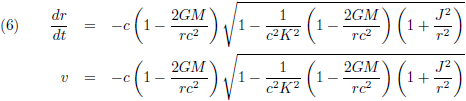
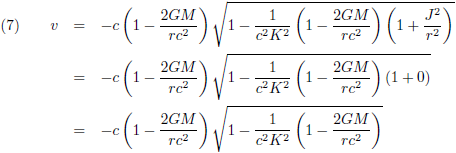
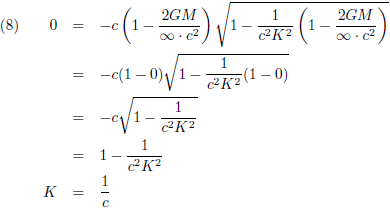
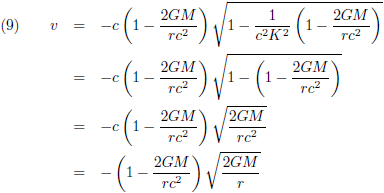
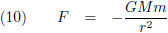
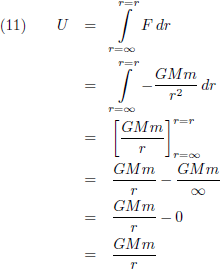
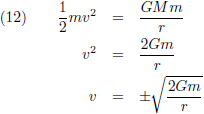
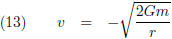
Ik breng de Schwarzschild-straal even in herinnering, de straal van een zwart gat:
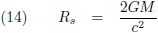
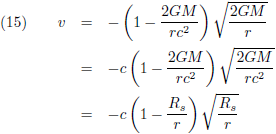
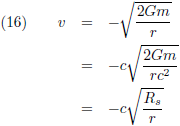
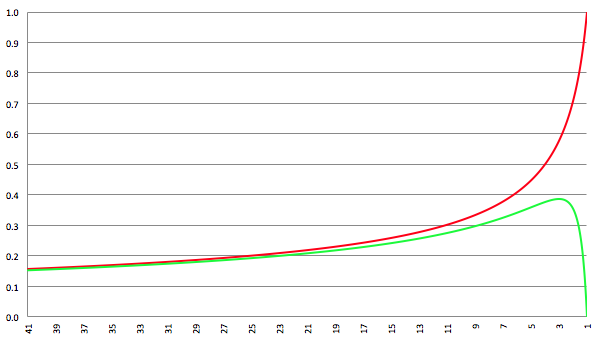
De grafiek van −v (r), klassiek (de rode lijn) en relativistisch (de groene lijn)
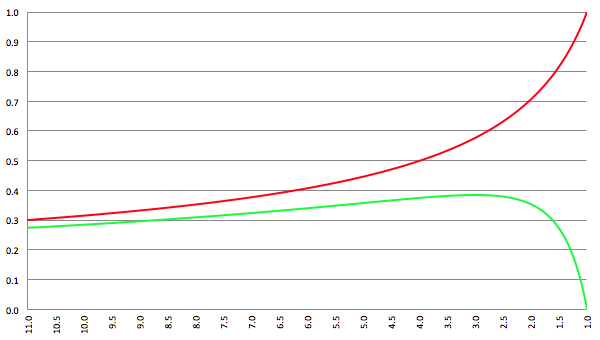
De grafiek van −v (r), klassiek (de rode lijn) en relativistisch (de groene lijn)
We zien ook dat de relativistische snelheid, de groene lijn, een maximum vertoont. Ik ga uitrekenen waar dit maximum ligt en daarvoor ga ik vergelijking (15) differentiëren naar r:
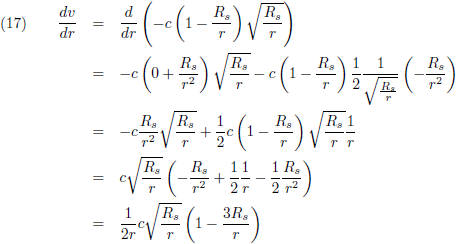
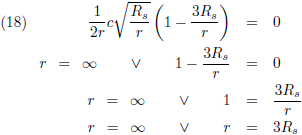
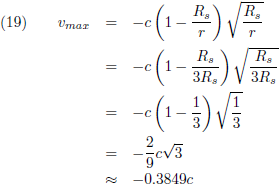
 Deze tabel geldt voor een niet-roterend zwart gat |
 Voor een verre stationaire waarnemer |
 Voor een nabije stationaire waarnemer |
 Voor een meebewegende waarnemer |
| De invaltijd van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
|
| De snelheid van een baksteen die in een zwart gat valt |
Toon uitwerking (= deze pagina) |
Toon uitwerking |
Toon uitwerking |
| De versnelling van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
Toon uitwerking |


 Door naar het volgende vraagstuk: de invaltijd van een baksteen die in een zwart gat valt
Door naar het volgende vraagstuk: de invaltijd van een baksteen die in een zwart gat valt Terug naar het vorige vraagstuk: de uitdijing van het heelal
Terug naar het vorige vraagstuk: de uitdijing van het heelal Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie Wat maakt een zwart gat tot een zwart gat?
Wat maakt een zwart gat tot een zwart gat? De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt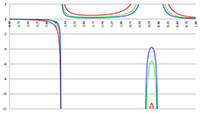 De integraal van
De integraal van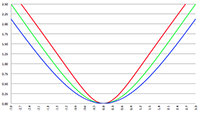 De integraal van
De integraal van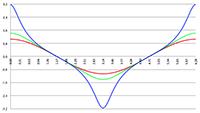 De integraal van
De integraal van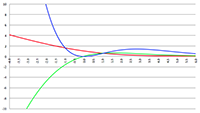 De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 26
Vectoren, vraagstuk 26 Vectoren, vraagstuk 64
Vectoren, vraagstuk 64 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT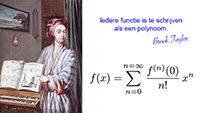 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen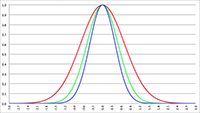 De Taylor-reeks van
De Taylor-reeks van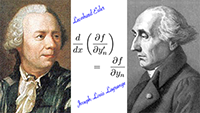 De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking Relativiteitstheorie rekenkundig
Relativiteitstheorie rekenkundig Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie
Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie Stabiliteit van cirkelvormige banen om een centrale massa
Stabiliteit van cirkelvormige banen om een centrale massa De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt Het Casimir-effect
Het Casimir-effect De grote vragen in het leven
De grote vragen in het leven Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen