De integraal van
f (x) = 1/(x2 (ax2 + bx + c))
Trefwoorden/keywords: integraal/integral, integreren/integrate, f (x) = 1/(x2 (ax2 + bx + c))
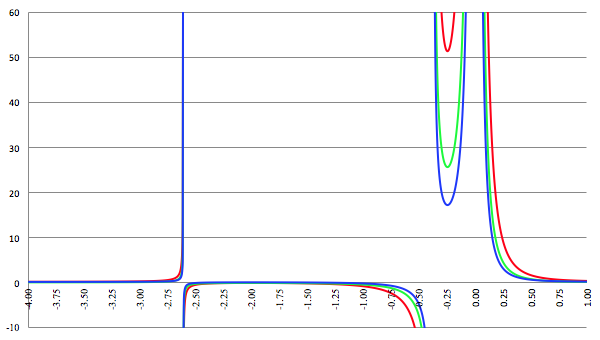
De grafiek van f (x) = 1/(x (ax
2 + bx + c)) voor a = 1, b = 3, c = 1 (de rode lijn),
a = 2, b = 6, c = 2 (de groene lijn) en a = 3, b = 9, c = 3 (de blauwe lijn)
Ik schrijf de functie iets anders op (waarbij r = 0 en s = 0):
Hierin zijn de nulpunten p en q:
De oplossing van deze
integraal
in deze vorm is elders terug te vinden in de
tabel met integralen.
De
integraal wordt dan:
Ik vul eerst r = 0 in:
Vervolgens wil ik s = 0 invullen, maar dat levert een probleem op (delen door nul).
Die bewuste term pak ik er even uit en neem ik apart onder handen:
In de
tabel met Taylor-reeksen vinden we:
Hiermee wordt de limiet voor s gaat naar nul:
Nu kan ik s = 0 invullen in het antwoord van de
integraal:
En ik vul de waarden voor p en q in om tot het eindresultaat te komen:
Ter controle ga ik het resultaat
differentiëren:
Tot slot wil ik nog opmerken dat je de
area tangens hyperbolicus
kunt
omschrijven naar een
natuurlijke logaritme,
en vice versa, als volgt:
De oplossing van deze
integraal
kan ik daarom ook als volgt opschrijven:

De grafiek van F (x) voor a = 1, b = 3, c = 1 (de rode lijn),
a = 2, b = 6, c = 2 (de groene lijn) en a = 3, b = 9, c = 3 (de blauwe lijn), C = 0










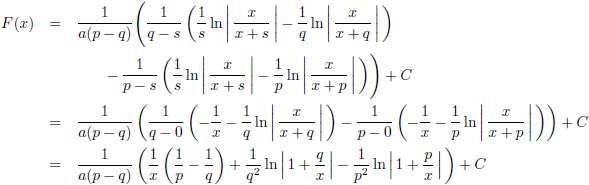





 Door naar de volgende integraal: de integraal van
Door naar de volgende integraal: de integraal van Terug naar de vorige integraal: de integraal van
Terug naar de vorige integraal: de integraal van Tabel met integralen
Tabel met integralen Tabel met afgeleiden
Tabel met afgeleiden Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De integralen van
De integralen van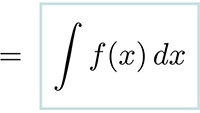 Integreren
Integreren Differentiëren
Differentiëren De afgeleide van
De afgeleide van Definities van hyperbolische functies
Definities van hyperbolische functies Machtsverheffen, worteltrekken, logaritme nemen
Machtsverheffen, worteltrekken, logaritme nemen Uitleg artikel algemene relativiteitstheorie: paragraaf 6
Uitleg artikel algemene relativiteitstheorie: paragraaf 6 De illusie van versheid
De illusie van versheid De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van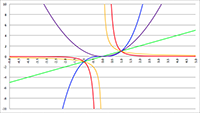 De integralen van
De integralen van Vectoren, vraagstuk 9
Vectoren, vraagstuk 9 Vectoren, vraagstuk 47
Vectoren, vraagstuk 47 Vectoren, vraagstuk 85
Vectoren, vraagstuk 85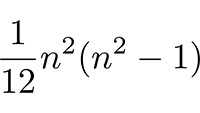 Onafhankelijke componenten in de Riemann-tensor
Onafhankelijke componenten in de Riemann-tensor De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van Getallen
Getallen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt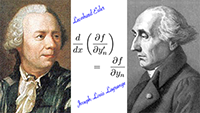 De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat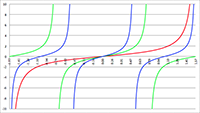 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)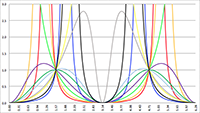 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2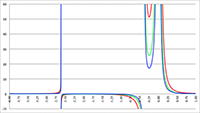 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen