Integreren


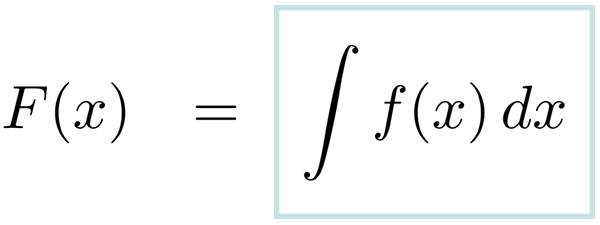
Zoals gezegd kun je met integreren oppervlakten en volumes berekenen. Stel dat ik van een functie het oppervlak wil bepalen tussen die functie en de x-as over de afstand van x = a tot x = b dan zijn a en b de integratiegrenzen van de integraal of kortweg de grenzen. Een integraal waarbij geen integratiegrenzen vermeld staan, zoals bij nagenoeg alle integralen op deze pagina, is een onbepaalde integraal. Zijn de grenzen wel bekend dan hebben we te maken met een bepaalde integraal en dat wordt als volgt genoteerd en uitgewerkt (ik bereken hier het oppervlak A tussen de functie y = x2 en de x-as over de afstand van x = 3 tot x = 5):

Terwijl het met differentiëren zo is dat je uiteindelijk altijd tot een afgeleide komt door simpelweg regeltjes te volgen (je kunt er gemakkelijk een computerprogramma voor schrijven), is het met integreren vaak totaal anders. Er is geen standaardmethode om een integraal aan te pakken, zodanig dat je altijd tot een oplossing komt. Maar er is wel een reeks handigheidjes die je kunt toepassen en die dan wellicht de sleutel vormen tot een oplossing.
-
De eerste truc heet kijken.
Dit klinkt heel flauw, maar soms lijkt het allemaal heel ingewikkeld en kun je door goed te kijken al de
oplossing zien.
Voorbeeld 1:Dit ziet er in eerste instantie wellicht ingewikkeld uit en je zou de neiging kunnen krijgen om die vijfde macht uit te werken om de haakjes kwijt te raken. Echter, in tweede instantie zie je dat die x2 de afgeleide is van x3 en dan wordt de oplossing heel simpel: Voorbeeld 2:
Voorbeeld 2: In eerste instantie wordt je wellicht een beetje paniekerig van deze functie, maar in tweede instantie zie je dat de teller de afgeleide is van de noemer en dan wordt de oplossing heel simpel:
In eerste instantie wordt je wellicht een beetje paniekerig van deze functie, maar in tweede instantie zie je dat de teller de afgeleide is van de noemer en dan wordt de oplossing heel simpel: Kortom, neem eerst de tabel met afgeleiden en de tabel met integralen ter hand en kijk ‘of het ergens op lijkt’. Als dat het geval is, dan zit je vaak al een heel eind in de goede richting.
Kortom, neem eerst de tabel met afgeleiden en de tabel met integralen ter hand en kijk ‘of het ergens op lijkt’. Als dat het geval is, dan zit je vaak al een heel eind in de goede richting.
-
De tweede truc heet breuksplitsing.
Dit is uiteraard alleen een mogelijk redmiddel wanneer je met een breuk te maken hebt.
Indien de noemer is te ontbinden in factoren dan is één van die factoren misschien uit te delen in de teller,
hetzij direct, hetzij indirect door nog wat aan de teller te sleutelen (door er
machten van x bij op te tellen
en gelijk weer vanaf te trekken).
Terwijl je met één breuk begon gaat het aantal breuken hierdoor wel toenemen, maar daarmee komt ook een
oplossing dichterbij.
Als de noemer niet is te ontbinden in factoren dan gaat breuksplitsing niet werken.
Voorbeeld 1:Voorbeeld 2:
 Voorbeeld 3:
Voorbeeld 3:



-
De derde truc heet goniometrische substitutie.
Deze methode kan heel handig zijn om
wortels kwijt te raken.
Door de variable x te vervangen door sin t, tan t of sec t krijgt het integratieprobleem ineens een hele andere vorm.
Heb je iets van de vorm √(a − x2) dan is de vervanging van x door sin t handig, heb je iets
van de vorm √(a + x2) dan is de vervanging door tan t handig en voor √(x2 − a)
kan vervanging door sec t redding brengen.
Voorbeeld 1:Voorbeeld 2:



-
De vierde truc heet partieel integreren.
Vanuit het differentiëren
kennen we de productregel
en die gebruiken we indien een functie bestaat uit het product van twee andere functies:
Oftewel:

 Dit kan ik ook anders opschrijven, waarbij ik gelijk de functie-van-x-aanduidingen weglaat:
Dit kan ik ook anders opschrijven, waarbij ik gelijk de functie-van-x-aanduidingen weglaat: Nu ga ik alles integreren:
Nu ga ik alles integreren: De integraal van de afgeleide is uiteraard weer de oorspronkelijke functie:
De integraal van de afgeleide is uiteraard weer de oorspronkelijke functie: En tenslotte bereik ik mijn einddoel door een integraal naar de andere kant te brengen:
En tenslotte bereik ik mijn einddoel door een integraal naar de andere kant te brengen: Ik zal wederom laten zien hoe dit in de praktijk uitwerkt.
Ik zal wederom laten zien hoe dit in de praktijk uitwerkt.
Voorbeeld 1:Voorbeeld 2:



 Tabel met integralen
Tabel met integralen Tabel met afgeleiden
Tabel met afgeleiden Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 5
Vectoren, vraagstuk 5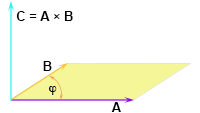 Vectoren, vraagstuk 43
Vectoren, vraagstuk 43 Vectoren, vraagstuk 81
Vectoren, vraagstuk 81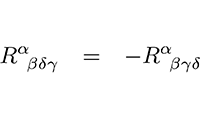 Anti-symmetrie in de Riemann-tensor
Anti-symmetrie in de Riemann-tensor De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van Matrices
Matrices Uitleg artikel algemene relativiteitstheorie: paragraaf 4
Uitleg artikel algemene relativiteitstheorie: paragraaf 4 Gelijktijdigheid
Gelijktijdigheid De maximale snelheid
De maximale snelheid De posities van de Lagrange-punten
De posities van de Lagrange-punten De potentialen van het elektromagnetische veld
De potentialen van het elektromagnetische veld De illusies die wij leven
De illusies die wij leven De illusie dat ik geen keus heb
De illusie dat ik geen keus heb Axiomahekken
Axiomahekken Het 5G-netwerk
Het 5G-netwerk Reacties op lezingen
Reacties op lezingen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen