De baan van een baksteen bij een zwart gat
Bereken alle mogelijke banen van een baksteen die ik naar een niet-roterend zwart gat gooi.
Omdat dit baksteenprobleem nogal een uitgebreid verhaal is heb ik het onderverdeeld in vijftien hoofdstukken
(als je zo veel mogelijk wiskunde wilt overslaan dan raad ik aan om gelijk naar hoofdstuk 5 te gaan):
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting
Afleidingen van de vergelijkingen
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting
Dit is de Schwarzschild-oplossing:










Onderzoek van de functie
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting
Om te beginnen breng ik de Schwarzschild-straal even in herinnering, de straal van een zwart gat:



 a < 0 |
 a > 0 |
| Tabel 1 | |

- D < 0: één nulpunt.
- D = 0: twee nulpunten,
- D > 0: drie nulpunten,
 D < 0 |
 D = 0 |
 D > 0 |
| Tabel 2 | ||


Figuur 1
De grafiek van D (E2) voor J = 1 (de rode lijn), J = √3 (de oranje lijn),
J = 3 (de groene lijn), J = 4 (de paarse lijn),
J = 5 (de blauwe lijn), J = 6 (de grijze lijn),
J = 7 (de bruine lijn) en J = 8 (de gele lijn),
Rs = 1




Figuur 2
De grafiek van E2 (J) voor de plusoplossing (de rode lijn)
en de minoplossing (de groene lijn),
D = 0, Rs = 1


Figuur 3
De grafiek van E (J) voor de plusoplossing (de rode lijn)
en de minoplossing (de groene lijn),
D = 0, Rs = 1

Ik kan in vergelijking (16a) ook aflezen waar D een maximum bereikt, de top van de parabool:





Ik ga vergelijking (13) anders opschrijven:


Figuur 4
De grafiek van D (J2) (alleen het deel tussen de haakjes)
voor E = 0.2 (de rode lijn), E = 0.3 (de oranje lijn),
E = 0.4 (de groene lijn), E = 0.5 (de paarse lijn),
E = 0.6 (de blauwe lijn), E = 0.7 (de grijze lijn),
E = 0.8 (de bruine lijn) en E = 0.9 (de gele lijn),
Rs = 1

Figuur 5
De grafiek van D (J2) (alleen het deel tussen de haakjes)
voor E = 1.1 (de rode lijn), E = 1.2 (de oranje lijn),
E = 1.3 (de groene lijn), E = 1.4 (de paarse lijn),
E = 1.5 (de blauwe lijn), E = 1.6 (de grijze lijn),
E = 1.7 (de bruine lijn) en E = 1.8 (de gele lijn),
Rs = 1




Figuur 6
De grafiek van J2 (E) voor de plusoplossing (de rode lijn)
en de minoplossing (de groene lijn),
D = 0, Rs = 1


Figuur 7
De grafiek van J (E) voor de plusoplossing (de rode lijn)
en de minoplossing (de groene lijn),
D = 0, Rs = 1

Ik kan in vergelijking (26a) ook aflezen waar D een maximum bereikt, de top van de parabool:








Figuur 8
De grafiek van E (J) = figuur 3 (links) en de grafiek van J (E) = figuur 7 (rechts),
D = 0, Rs = 1

Figuur 9
De grafiek van E (J),
D = 0, Rs = 1

Figuur 10
De grafiek van J (E),
D = 0, Rs = 1

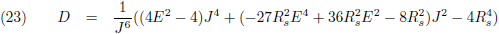

Figuur 11
De grafiek van D (J2)
voor E = 0 (de rode lijn), E = 0.25 (de oranje lijn),
E = 0.5 (de groene lijn), E = 0.75 (de paarse lijn),
E = 1 (de blauwe lijn), E = 1.25 (de grijze lijn),
E = 1.5 (de bruine lijn) en E = 1.75 (de gele lijn),
Rs = 1

Figuur 12
De grafiek van D (E, J),
Rs = 1
De effectieve potentiaal
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting






Figuur 13
De grafiek van V (r) voor J = 0.0 (de rode lijn),
J = 0.5 (de lichtgroene lijn), J = 1.0 (de oranje lijn),
J = 1.5 (de paarse lijn), J = √3 (de blauwe lijn),
J = 2.0 (de grijze lijn), J = 2.5 (de bruine lijn),
J = 3.0 (de lichtbruine lijn), J = 3.5 (de donkergroene lijn),
J = 4.0 (de gele lijn) en J = 4.5 (de lichtblauwe lijn),
Rs = 1

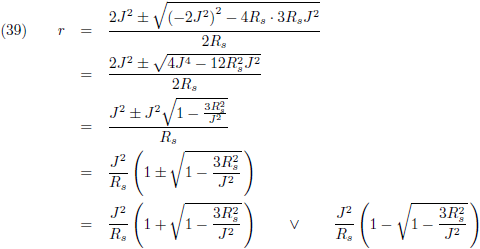

Figuur 14
De grafiek van V (r) voor J = 0.0 (de rode lijn),
J = 0.5 (de lichtgroene lijn), J = 1.0 (de oranje lijn),
J = 1.5 (de paarse lijn), J = √3 (de blauwe lijn),
J = 2.0 (de grijze lijn), J = 2.5 (de bruine lijn),
J = 3.0 (de lichtbruine lijn), J = 3.5 (de donkergroene lijn),
J = 4.0 (de gele lijn) en J = 4.5 (de lichtblauwe lijn),
de zwarte punten zijn de extrema volgens vergelijking (39),
Rs = 1

Figuur 15
De grafiek van V (r) voor J = 0.0 (de rode lijn),
J = 0.5 (de lichtgroene lijn), J = 1.0 (de oranje lijn),
J = 1.5 (de paarse lijn), J = √3 (de blauwe lijn),
J = 2.0 (de grijze lijn), J = 2.5 (de bruine lijn),
J = 3.0 (de lichtbruine lijn), J = 3.5 (de donkergroene lijn),
J = 4.0 (de gele lijn) en J = 4.5 (de lichtblauwe lijn),
de zwarte punten zijn de nulpunten volgens vergelijking (39),
Rs = 1

Nulpunten in de noemer
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting





 D < 0 |
Eén nulpunt: |
 D = 0 |
Twee nulpunten, een snijpunt en een raakpunt (het raakpunt is feitelijk twee samenvallende nulpunten):   Indien q'' > 0 dan ligt het raakpunt rechts van het snijpunt en indien q'' < 0 dan ligt het raakpunt links van het snijpunt. |
 D > 0 |
Drie nulpunten, van links naar rechts:   |
| Tabel 3 | |




Radiële inval
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting


Figuur 16
De grafiek van φ (x, y) voor φ0 = 0,
J = 0, Rs = 1

Figuur 17
De grafiek van φ (x, y) voor φ0 = π/6,
J = 0, Rs = 1
| Condities | Baan van de baksteen |
| J = 0 | De baksteen valt radieel in het
zwarte gat (0 < u < 1/Rs oftewel Rs < r < ∞)   |
| Tabel 4 | |
Invallende banen vanaf ‘ver weg’ (D < 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting


Deze oplossing is bereikt door de integraal om te schrijven naar een elliptische integraal van de eerste soort. Je ziet in de oplossing dat de oorspronkelijke variabelen onherkenbaar veranderd zijn doordat er onderweg talrijke transformaties hebben plaatsgevonden, maar het ergste is dat de oplossing in dit geval (ruimschoots) onvoldoende praktisch nut heeft omdat de oplossing tot stand gekomen is middels een Taylor-reeks. Willen we daarmee verder werken dan zullen we vele duizenden termen mee moeten nemen en dat wordt zelfs voor de computer (mijn computer) een onhaalbare rekenexercitie.
Daarom ga ik het heel anders aanpakken en ga ik voor het uitwerken van de integraal gebruik maken van de trapeziummethode:
In een simpel geval dat het inkomende object nauwelijks impulsmoment heeft dan ziet het resultaat er als volgt uit, vergelijkbaar met de radiële inval.

Figuur 18
De grafiek van φ (x, y) voor J = 0.1,
D = −7.044 ∙ 106, E = 2.0117769801886, n1 = −2.761, Rs = 1,
999.999 intervallen

Figuur 19
De grafiek van φ (x, y) voor J = 2,
D = −16.051, E = 2.0117769801886, n1 = −0.614, Rs = 1,
999.999 intervallen

Figuur 20
De grafiek van φ (x, y) voor J = 3,
D = −2.411, E = 2.0117769801886, n1 = −0.447, Rs = 1,
999.999 intervallen

Figuur 21
De grafiek van φ (x, y) voor J = 4,
D = −0.429, E = 2.0117769801886, n1 = −0.353, Rs = 1,
999.999 intervallen

Figuur 22
De grafiek van φ (x, y) voor J = 4.9,
D = −0.021, E = 2.0117769801886, n1 = −0.297, Rs = 1,
9.999.999 intervallen


Figuur 23
De grafiek van g (u) voor J = 3 (de rode lijn)
in stappen van 0.2 oplopend tot J = 5 (de lichtblauwe lijn),
E = 2.01177698018854, Rs = 1


Figuur 24
De grafiek van f (u) voor J = 3 (de rode lijn)
in stappen van 0.2 oplopend tot J = 5 (de lichtblauwe lijn),
E = 2.01177698018854, Rs = 1

Figuur 25
De grafiek van φ (x, y) voor J = 5,
D = −3.125 ∙ 10−14, E = 2.0117769801886, n1 = −0.292, Rs = 1,
5 rondjes om het zwarte gat,
40.959.718 intervallen

Figuur 26
De grafiek van φ (x, y) voor J = 5,
D = −3.125 ∙ 10−14, E = 2.0117769801886, n1 = −0.292, Rs = 1,
5 rondjes om het zwarte gat,
40.959.718 intervallen

Figuur 27
De grafiek van φ (x, y) voor J = 5,
D = −3.125 ∙ 10−14, E = 2.0117769801886, n1 = −0.292, Rs = 1,
5 rondjes om het zwarte gat,
40.959.718 intervallen

Figuur 28
De grafiek van φ (x, y) voor J = 5,
D = −4.428 ∙ 10−21, E = 2.01177698018854097539, n1 = −0.292, Rs = 1,
7.5 rondjes om het zwarte gat,
192.772.784 intervallen

Figuur 29
De grafiek van E (J), D = 0, Rs = 1,
met daarin de punten (de groene bolletjes) van de voorgaande figuren
Invallende banen vanaf ‘dichtbij’ (D < 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting



Figuur 30
De grafiek van g (u) voor E = 0 (de rode lijn)
in stappen van 0.2 oplopend tot E = 2 (de lichtblauwe lijn),
de grijze lijn is E = 1,
J = 1, Rs = 1

Figuur 31
De grafiek van f (u) voor E = 0 (de rode lijn)
in stappen van 0.2 oplopend tot E = 2 (de lichtblauwe lijn),
de grijze lijn is E = 1,
J = 1, Rs = 1

Figuur 32
De grafiek van f (u) voor E = 0 (de rode lijn)
in stappen van 0.2 oplopend tot E = 2 (de lichtblauwe lijn),
de grijze lijn is E = 1,
J = 1, Rs = 1

Figuur 35
De grafiek van φ (x, y) voor E = 0.8,
D = −1.459, J = 1, n1 = 0.480, 1/n1 = 2.084, Rs = 1,
9.999.999 intervallen

Figuur 36
De grafiek van φ (x, y) voor E = 0.9,
D = −1.315, J = 1, n1 = 0.231, 1/n1 = 4.328, Rs = 1,
9.999.999 intervallen

Figuur 37
De grafiek van φ (x, y) voor E = 0.95,
D = −1.892, J = 1, n1 = 0.108, 1/n1 = 9.269, Rs = 1,
9.999.999 intervallen
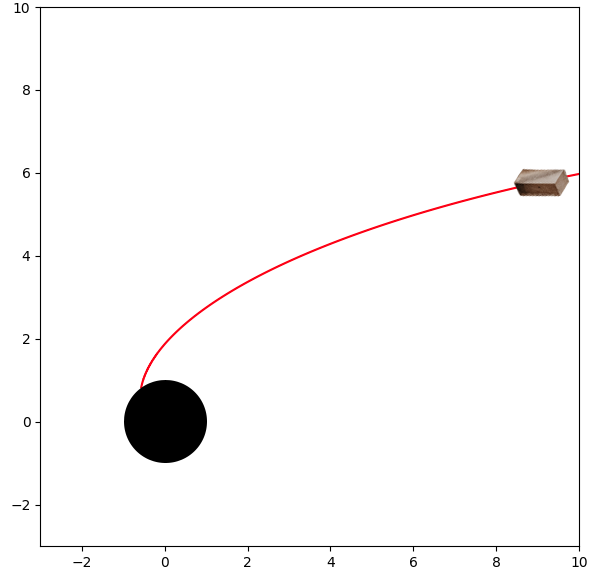
Figuur 38
De grafiek van φ (x, y) voor E = 0.99,
D = −2.732, J = 1, n1 = 0.020, 1/n1 = 49.252, Rs = 1,
9.999.999 intervallen

Figuur 39
De grafiek van φ (x, y) voor E = 0.999,
D = −2.972, J = 1, n1 = 0.002, 1/n1 = 499.250, Rs = 1,
9.999.999 intervallen

Figuur 40
De grafiek van f (u) voor E = 0.1 (de oranje lijn)
in stappen van 0.1 oplopend tot E = 1 (de lichtblauwe lijn),
J = 5, Rs = 1

Figuur 41
De grafiek van f (u) voor E = 0.1 (de oranje lijn)
in stappen van 0.1 oplopend tot E = 1 (de lichtblauwe lijn),
J = 5, Rs = 1

Figuur 42
De grafiek van φ (x, y) voor E = 0.9,
D = −0.025, J = 5, n1 = 0.967, 1/n1 = 1.034, Rs = 1,
9.999.999 intervallen

Figuur 43
De grafiek van E (J), D = 0, Rs = 1

Figuur 44
De grafiek van g (u) voor J = 1.6 de rode lijn)
in stappen van 0.06 oplopend tot J = 2.2 (de lichtblauwe lijn),
E = 0.999, Rs = 1

Figuur 45
De grafiek van f (u) voor J = 1.6 de rode lijn)
in stappen van 0.06 oplopend tot J = 2.2 (de lichtblauwe lijn),
E = 0.999, Rs = 1
| Condities | Baan van de baksteen | |
| J = 0 | De baksteen valt radieel in het
zwarte gat (0 < u < 1/Rs oftewel Rs < r < ∞)   |
|
| D < 0 | E ≥ 1 | De baksteen eindigt in het
zwarte gat vanaf ‘ver weg’ (0 < u < 1/Rs oftewel Rs < r < ∞)    |
| E < 1 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n1 < u < 1/Rs oftewel Rs < r < 1/n1)    |
|
| Tabel 5 | ||
Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting
 q'' < 0 |
 q'' > 0 |
| Tabel 6 | |





Figuur 46
De grafiek van q'' (J) voor de plusoplossing (de rode lijn)
en de minoplossing (de groene lijn),
D = 0, Rs = 1






Figuur 47
De grafiek van q'' (E) voor de minoplossing (de rode lijn)
en de plusoplossing (de groene lijn),
D = 0, Rs = 1

Figuur 48
De grafiek van E (J),
D = 0, Rs = 1

Figuur 49
De grafiek van J (E),
D = 0, Rs = 1



Figuur 50
De grafiek van n1 (J) (de minoplossing, de rode lijn),
n1 (J) (de plusoplossing, de oranje lijn),
n2/3 (J) (de plusoplossing, de groene lijn)
en n2/3 (J) (de minoplossing, de paarse lijn),
Rs = 1








Figuur 52
De grafiek van φ (x, y) voor J = 3, E = 0.9851121580978086,
D = 0, n1 = 0.878, 1/n1 = 1.139, q'' = −2.016 ∙ 10−2, Rs = 1,
1.000.002 datapunten

Figuur 53
De grafiek van φ (x, y) voor J = 2, E = 0.9622504486493763,
D = 0, n1 = 0.667, 1/n1 = 1.500, q'' = −4.630 ∙ 10−3, Rs = 1,
1.000.002 datapunten

Figuur 54
De grafiek van φ (x, y) voor J = 1.9, E = 0.9568176372873567,
D = 0, n1 = 0.607, 1/n1 = 1.646, q'' = −2.573 ∙ 10−3, Rs = 1,
1.000.001 datapunten

Figuur 55
De grafiek van φ (x, y) voor J = 1.8, E = 0.9496463385962782,
D = 0, n1 = 0.515, 1/n1 = 1.943, q'' = −7.467 ∙ 10−4, Rs = 1,
1.000.002 datapunten

Figuur 56
De grafiek van φ (x, y) voor J = 1.7321, E = 0.9428156854432492,
D = 0, n1 = 0.338, 1/n1 = 2.955, q'' = −1.585 ∙ 10−8, Rs = 1,
5 rondjes om het zwarte gat,
249.999.998 datapunten

Figuur 57
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D = 0, Rs = 1

Figuur 58
De grafiek van φ (x, y) voor J = 1.7320508076, E = 0.9428090415862986,
D = 0, n1 = 0.333337, 1/n1 = 2.999964, q'' = −7.979 ∙ 10−18, Rs = 1,
173.5 rondjes om het zwarte gat,
400.000.000 datapunten
Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting

Figuur 59
De grafiek van g (u) met een snijpunt n1 = 0.5
en een raakpunt n2/3 = 3

Figuur 60
De grafiek van f (u) met een snijpunt n1 = 0.5
en een raakpunt n2/3 = 3

Figuur 61
Het traject waar de integrand f (u) bestaat (de oranje balk),
D = 0, E ≥ 1, q'' > 0

Figuur 62
Het traject waar de integrand f (u) bestaat (de oranje balk),
D = 0, E ≥ 1, q'' > 0

Figuur 63
Het traject waar de integrand f (u) bestaat (de oranje balk),
D = 0, E < 1, q'' > 0








Figuur 64
De grafiek van φ (x, y) voor J = 4, E = 1.6491982708836967,
D = 0, n1 = −0.268, n2/3 = 0.634, 1/n2/3 = 1.578, q'' = 2.713 ∙ 10−2, Rs = 1,
3 rondjes om het zwarte gat,
27.365.598 datapunten

Figuur 65
De grafiek van φ (x, y) voor J = 2.5, E = 1.141591103064672,
D = 0, n1 = −0.147, n2/3 = 0.574, 1/n2/3 = 1.743, q'' = 1.389 ∙ 10−2, Rs = 1,
3.5 rondjes om het zwarte gat,
29.187.870 datapunten

Figuur 66
De grafiek van φ (x, y) voor J = 2.1, E = 1.025861056739398,
D = 0, n1 = −0.044, n2/3 = 0.522, 1/n2/3 = 1.916, q'' = 6.696 ∙ 10−3, Rs = 1,
4 rondjes om het zwarte gat,
31.099.521 datapunten

Figuur 67
De grafiek van φ (x, y) voor J = 1.9, E = 0.9760369650397409,
D = 0, n1 = 0.059, 1/n1 = 16.866, n2/3 = 0.470, 1/n2/3 = 2.126, q'' = 2.573 ∙ 10−3, Rs = 1,
5 rondjes om het zwarte gat,
159.499.431 datapunten

Figuur 68
De grafiek van φ (x, y) voor J = 1.8, E = 0.954727796245619,
D = 0, n1 = 0.152, 1/n1 = 6.584, n2/3 = 0.424, 1/n2/3 = 2.358, q'' = 7.467 ∙ 10−4, Rs = 1,
6 rondjes om het zwarte gat,
61.426.903 datapunten

Figuur 69
De grafiek van φ (x, y) voor J = 1.7321, E = 0.9428157863474071,
D = 0, n1 = 0.328, 1/n1 = 3.046, n2/3 = 0.336, 1/n2/3 = 2.978, q'' = 1.585 ∙ 10−8, Rs = 1,
30.5 rondjes om het zwarte gat,
475.377.539 datapunten

Figuur 70
De grafiek van E (J), D = 0, Rs = 1,
met daarin de punten (de groene bolletjes) van de voorgaande figuren
Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting








Figuur 71
De grafiek van φ (x, y) voor J = 4, E = 1.6491982708836967,
D = 0, n1 = −0.268, n2/3 = 0.634, 1/n2/3 = 1.578, q'' = 2.713 ∙ 10−2, Rs = 1,
2 rondjes om het zwarte gat,
400.000.030 datapunten

Figuur 72
De grafiek van φ (x, y) voor J = 2.5, E = 1.141591103064672,
D = 0, n1 = −0.147, n2/3 = 0.574, 1/n2/3 = 1.743, q'' = 1.389 ∙ 10−2, Rs = 1,
2.5 rondjes om het zwarte gat,
400.000.022 datapunten

Figuur 73
De grafiek van φ (x, y) voor J = 2.1, E = 1.025861056739398,
D = 0, n1 = −0.044, n2/3 = 0.522, 1/n2/3 = 1.916, q'' = 6.696 ∙ 10−3, Rs = 1,
2.5 rondjes om het zwarte gat,
399.999.997 datapunten

Figuur 74
De grafiek van φ (x, y) voor J = 1.9, E = 0.9760369650397409,
D = 0, n1 = 0.059, 1/n1 = 16.866, n2/3 = 0.470, 1/n2/3 = 2.126, q'' = 2.573 ∙ 10−3, Rs = 1,
3.5 rondjes om het zwarte gat,
399.999.999 datapunten

Figuur 75
De grafiek van φ (x, y) voor J = 1.8, E = 0.954727796245619,
D = 0, n1 = 0.152, 1/n1 = 6.584, n2/3 = 0.424, 1/n2/3 = 2.358, q'' = 7.467 ∙ 10−4, Rs = 1,
4 rondjes om het zwarte gat,
400.000.012 datapunten

Figuur 76
De grafiek van φ (x, y) voor J = 1.7321, E = 0.9428157863474071,
D = 0, n1 = 0.328, 1/n1 = 3.046, n2/3 = 0.336, 1/n2/3 = 2.978, q'' = 1.585 ∙ 10−8, Rs = 1,
20.5 rondjes om het zwarte gat,
399.999.995 datapunten

Figuur 77
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D = 0, Rs = 1

Figuur 78
(= figuur 64 (de blauwe lijn) + figuur 71 (de rode lijn))
De grafiek van φ (x, y) voor J = 4, E = 1.6491982708836967,
D = 0, n1 = −0.268, n2/3 = 0.634, 1/n2/3 = 1.578, q'' = 2.713 ∙ 10−2, Rs = 1,
427.365.628 datapunten

Figuur 79
(= figuur 65 (de blauwe lijn) + figuur 72 (de rode lijn))
De grafiek van φ (x, y) voor J = 2.5, E = 1.141591103064672,
D = 0, n1 = −0.147, n2/3 = 0.574, 1/n2/3 = 1.743, q'' = 1.389 ∙ 10−2, Rs = 1,
429.187.892 datapunten

Figuur 80
(= figuur 66 (de blauwe lijn) + figuur 73 (de rode lijn))
De grafiek van φ (x, y) voor J = 2.1, E = 1.025861056739398,
D = 0, n1 = −0.044, n2/3 = 0.522, 1/n2/3 = 1.916, q'' = 6.696 ∙ 10−3, Rs = 1,
431.099.518 datapunten

Figuur 81
(= figuur 67 (de blauwe lijn) + figuur 74 (de rode lijn))
De grafiek van φ (x, y) voor J = 1.9, E = 0.9760369650397409,
D = 0, n1 = 0.059, 1/n1 = 16.866, n2/3 = 0.470, 1/n2/3 = 2.126, q'' = 2.573 ∙ 10−3, Rs = 1,
559.499.430 datapunten

Figuur 82
(= figuur 68 (de blauwe lijn) + figuur 75 (de rode lijn))
De grafiek van φ (x, y) voor J = 1.8, E = 0.954727796245619,
D = 0, n1 = 0.152, 1/n1 = 6.584, n2/3 = 0.424, 1/n2/3 = 2.358, q'' = 7.467 ∙ 10−4, Rs = 1,
461.426.915 datapunten

Figuur 83
(= figuur 69 (de blauwe lijn) + figuur 76 (de rode lijn))
De grafiek van φ (x, y) voor J = 1.7321, E = 0.9428157863474071,
D = 0, n1 = 0.328, 1/n1 = 3.046, n2/3 = 0.336, 1/n2/3 = 2.978, q'' = 1.585 ∙ 10−8, Rs = 1,
875.377.534 datapunten




Figuur 14
De grafiek van V (r) voor J = 0.0 (de rode lijn) oplopend tot J = 4.5 (de lichtblauwe lijn),
de zwarte punten zijn de extrema volgens vergelijking (39),
Rs = 1
Ik kan mijn tabel met conclusies weer uitbreiden.
| Condities | Baan van de baksteen | |||
| J = 0 | De baksteen valt radieel in het
zwarte gat (0 < u < 1/Rs oftewel Rs < r < ∞)   |
|||
| D < 0 | E ≥ 1 | De baksteen eindigt in het
zwarte gat vanaf ‘ver weg’ (0 < u < 1/Rs oftewel Rs < r < ∞)    |
||
| E < 1 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n1 < u < 1/Rs oftewel Rs < r < 1/n1)    |
|||
| D = 0 | q'' < 0 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n1 < u < 1/Rs oftewel Rs < r < 1/n1)    |
||
| q'' > 0 | E ≥ 1 | u > n2/3 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n2/3 < u < 1/Rs oftewel Rs < r < 1/n2/3)    |
|
| u < n2/3 | De baksteen eindigt in een baan om het
zwarte gat vanaf ‘dichtbij’ (n1 < u < n2/3 oftewel 1/n2/3 < r < 1/n1)    |
|||
| E < 1 | De baksteen eindigt in een baan om het
zwarte gat vanaf ‘ver weg’ (0 < u < n2/3 oftewel 1/n2/3 < r < ∞)    |
|||
| Tabel 7 | ||||
Invallende banen vanaf ‘dichtbij’ (D > 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting

Figuur 84
De grafiek van g (u) voor D > 0

Figuur 85
Het traject waar de integrand f (u) bestaat (de oranje balk),
D > 0, E ≥ 1, u > n3

Figuur 86
Het traject waar de integrand f (u) bestaat (de oranje balk),
D > 0, E ≥ 1, u < n2

Figuur 87
Het traject waar de integrand f (u) bestaat (de oranje balk),
D > 0, E < 1, n1 < u < n2






Binnen het domein “D > 0” ga ik een aantal punten eruit pikken en daarvoor de baan van de baksteen uitrekenen. Omdat u > n3 en dus 1/n3 < r < Rs zijn dit allemaal trajecten waarbij de baksteen in het zwarte gat eindigt (dit project kost een hoop bakstenen...).

Figuur 88
De grafiek van φ (x, y) voor E = 1.0, J = 5.0,
D = 1.344 ∙ 10−3, n1 = 5.551 ∙ 10−17, 1/n1 = 1.801 ∙ 1016,
n2 = 0.0417, 1/n2 = 23.956, n3 = 0.958, 1/n3 = 1.044, Rs = 1,
999.999 intervallen

Figuur 89
De grafiek van φ (x, y) voor E = 1.5, J = 5.0,
D = 9.784 ∙ 10−2, n1 = −0.189,
n2 = 0.297, 1/n2 = 3.372, n3 = 0.892, 1/n3 = 1.121, Rs = 1,
999.999 intervallen

Figuur 90
De grafiek van φ (x, y) voor E = 2.0, J = 5.0,
D = 6.144 ∙ 10−3, n1 = −0.290,
n2 = 0.600, 1/n2 = 1.667, n3 = 0.690, 1/n3 = 1.449, Rs = 1,
999.999 intervallen

Figuur 91
De grafiek van φ (x, y) voor E = 1.0, J = 4.0,
D = 2.930 ∙ 10−3, n1 = 1.665 ∙ 10−16, 1/n1 = 6.005 ∙ 1015,
n2 = 0.0670, 1/n2 = 14.928, n3 = 0.933, 1/n3 = 1.072, Rs = 1,
999.999 intervallen

Figuur 92
De grafiek van φ (x, y) voor E = 1.5, J = 4.0,
D = 6.274 ∙ 10−2, n1 = −0.228,
n2 = 0.428, 1/n2 = 2.334, n3 = 0.800, 1/n3 = 1.251, Rs = 1,
999.999 intervallen

Figuur 93
De grafiek van φ (x, y) voor E = 1.1, J = 3.0,
D = 3.883 ∙ 10−2, n1 = −0.104,
n2 = 0.271, 1/n2 = 3.696, n3 = 0.833, 1/n3 = 1.201, Rs = 1,
999.999 intervallen

Figuur 94
De grafiek van φ (x, y) voor E = 1.0, J = 2.1,
D = 4.780 ∙ 10−3, n1 = 0, 1/n1 = ∞,
n2 = 0.348, 1/n2 = 2.877, n3 = 0.652, 1/n3 = 1.533, Rs = 1,
999.999 intervallen

Figuur 95
De grafiek van φ (x, y) voor E = 0.98, J = 2.0,
D = 2.304 ∙ 10−3, n1 = 0.0486, 1/n1 = 20.584;,
n2 = 0.326, 1/n2 = 3.071, n3 = 0.626, 1/n3 = 1.598, Rs = 1,
999.999 intervallen
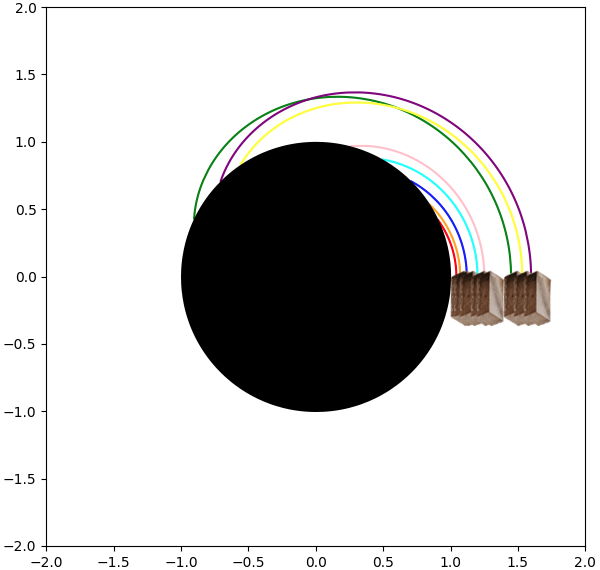
Figuur 96
De grafieken van φ (x, y) voor D > 0, u > n3, Rs = 1,
999.999 intervallen (per lijn)

Figuur 97
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D > 0, u > n3, Rs = 1
Stabiele open banen (D > 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting

Figuur 98
De grafiek van φ (x, y) voor E = 1.01 (de rode lijn), E = 1.1 (de blauwe lijn),
E = 1.2 (de groene lijn), E = 1.3 (de oranje lijn),
E = 1.4 (de roze lijn), E = 1.5 (de lichtblauwe lijn),
E = 1.6 (de gele lijn), E = 1.7 (de paarse lijn),
E = 1.8 (de bruine lijn) en E = 1.9 (de grijze lijn),
J = 5, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 99
De grafiek van φ (x, y) voor E = 2.0 (de rode lijn), E = 2.01 (de blauwe lijn),
E = 2.011 (de groene lijn), E = 2.0117 (de oranje lijn)
en E = 2.01177 (de grijze lijn),
J = 5, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 100
De grafiek van φ (x, y) voor E = 2.0 (de rode lijn, 0.5 rondje),
E = 2.01 (de blauwe lijn, 1 rondje),
E = 2.011 (de groene lijn, 1 rondje),
E = 2.0117 (de oranje lijn, 1.5 rondjes)
en E = 2.01177 (de grijze lijn, 2 rondjes),
J = 5, Rs = 1,
1.999.997 intervallen (per lijn)








Figuur 102
De grafiek van φ (x, y) voor E = 1.1, J = 5.00 (de blauwe lijn),
E = 1.2, J = 7.24 (de groene lijn), E = 1.3, J = 9.06 (de oranje lijn),
E = 1.4, J = 10.69 (de roze lijn), E = 1.5, J = 12.20 (de lichtblauwe lijn),
E = 1.6, J = 13.63 (de gele lijn), E = 1.7, J = 15.00 (de paarse lijn),
E = 1.8, J = 16.33 (de bruine lijn) en E = 1.9, J = 17.63 (de grijze lijn),
Rs = 1,
1.999.997 intervallen (per lijn)
De volgende plaatjes zijn met een constant impulsmoment en een variërende energie. Ik begin met J = 4 en laat die vervolgens stapsgewijs dalen (en om de plaatjes overzichtelijk te houden laat ik de bakstenen tijdelijk weg).

Figuur 103
De grafiek van φ (x, y) voor E = 1.01 (de rode lijn), E = 1.1 (de blauwe lijn),
E = 1.2 (de groene lijn), E = 1.3 (de oranje lijn),
E = 1.4 (de roze lijn), E = 1.5 (de lichtblauwe lijn),
E = 1.6 (de gele lijn), E = 1.64 (de paarse lijn),
E = 1.649 (de bruine lijn), E = 1.6491 (de grijze lijn)
en E = 1.64919 (de lichtgroene lijn),
J = 4, Rs = 1,
1.999.997 intervallen (per lijn)
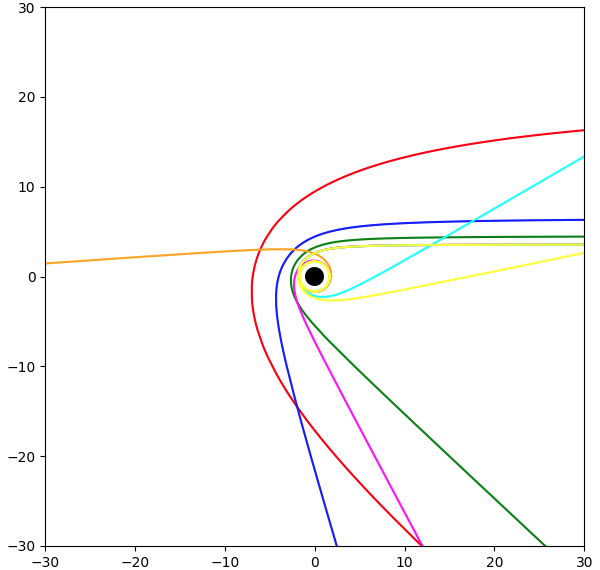
Figuur 104
De grafiek van φ (x, y) voor E = 1.01 (de rode lijn), E = 1.1 (de blauwe lijn),
E = 1.2 (de groene lijn), E = 1.3 (de oranje lijn),
E = 1.302 (de roze lijn), E = 1.3023 (de lichtblauwe lijn),
en E = 1.30239 (de gele lijn),
J = 3, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 105
De grafiek van φ (x, y) voor E = 1.01 (de rode lijn), E = 1.05 (de blauwe lijn),
E = 1.10 (de groene lijn), E = 1.14 (de oranje lijn),
E = 1.141 (de roze lijn), E = 1.1415 (de lichtblauwe lijn),
en E = 1.14159 (de gele lijn),
J = 2.5, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 106
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D > 0, E ≥ 1, u < n2, Rs = 1
Stabiele gesloten banen (D > 0)
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting

Figuur 9
De grafiek van E (J),
D = 0, Rs = 1

Figuur 107
De grafiek van E (J),
D = 0, Rs = 1

Figuur 108
De grafiek van φ (x, y) voor E = 0.995 (de rode lijn), E = 0.996 (de blauwe lijn),
E = 0.997 (de groene lijn), E = 0.998 (de oranje lijn),
en E = 0.999 (de paarse lijn),
J = 5, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 109
De grafiek van φ (x, y) voor E = 0.994882114, J = 5, Rs = 1,
1.999.997 intervallen
Het derde dat opvalt in figuur 108 is duidelijk zichtbaar bij de blauwe lijn: de baan sluit niet na één omwenteling om het zwarte gat, de baan precesseert! Ik pik die blauwe baan er even uit en laat de baksteen tien rondjes om het zwarte gat maken hetgeen de precessie overduidelijk zichtbaar maakt.

Figuur 110
De grafiek van φ (x, y) voor E = 0.996, J = 5, Rs = 1,
10 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 111
De grafiek van φ (x, y) voor E = 0.996, J = 5, Rs = 1,
50 rondjes om het zwarte gat,
99.999.899 intervallen

Figuur 112
De grafiek van φ (x, y) voor E = 0.992 (de rode lijn), E = 0.993 (de blauwe lijn),
E = 0.994 (de groene lijn), E = 0.995 (de oranje lijn),
E = 0.996 (de paarse lijn), E = 0.997 (de roze lijn),
E = 0.998 (de lichtblauwe lijn) en E = 0.999 (de gele lijn),
J = 4, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 113
De grafiek van φ (x, y) voor E = 0.995, J = 4, Rs = 1,
10 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 114
De grafiek van φ (x, y) voor E = 0.995, J = 4, Rs = 1,
50 rondjes om het zwarte gat,
99.999.899 intervallen

Figuur 115
De grafiek van φ (x, y) voor E = 0.986 (de rode lijn), E = 0.988 (de blauwe lijn),
E = 0.990 (de groene lijn), E = 0.992 (de oranje lijn),
E = 0.994 (de paarse lijn), E = 0.996 (de roze lijn)
en E = 0.998 (de lichtblauwe lijn),
J = 3, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 116
De grafiek van φ (x, y) voor E = 0.978 (de rode lijn), E = 0.980 (de blauwe lijn),
E = 0.982 (de groene lijn), E = 0.984 (de oranje lijn),
E = 0.986 (de paarse lijn), E = 0.988 (de roze lijn),
E = 0.990 (de lichtblauwe lijn), E = 0.992 (de gele lijn),
E = 0.994 (de lichtgroene lijn), E = 0.996 (de bruine lijn)
en E = 0.998 (de grijze lijn),
J = 2.5, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 117
De grafiek van φ (x, y) voor E = 0.963 (de rode lijn), E = 0.969 (de blauwe lijn),
E = 0.975 (de groene lijn), E = 0.981 (de oranje lijn),
E = 0.987 (de paarse lijn), E = 0.993 (de roze lijn)
en E = 0.999 (de lichtblauwe lijn),
J = 2, Rs = 1,
1.999.997 intervallen (per lijn)

Figuur 118
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D > 0, E < 1, u < n2, Rs = 1

Figuur 119
De grafiek van φ (x, y) voor E = 0.97, J = 1.9, Rs = 1,
1.8 rondjes om het zwarte gat,
1.999.997 intervallen

Figuur 120
De grafiek van φ (x, y) voor E = 0.97, J = 1.9, Rs = 1,
10 × 1.8 = 18 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 121
De grafiek van φ (x, y) voor E = 0.976, J = 1.9, Rs = 1,
3 rondjes om het zwarte gat,
1.999.997 intervallen

Figuur 122
De grafiek van φ (x, y) voor E = 0.976, J = 1.9, Rs = 1,
10 × 3 = 30 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 123
De grafiek van φ (x, y) voor E = 0.97603696, J = 1.9, Rs = 1,
5 rondjes om het zwarte gat,
1.999.997 intervallen
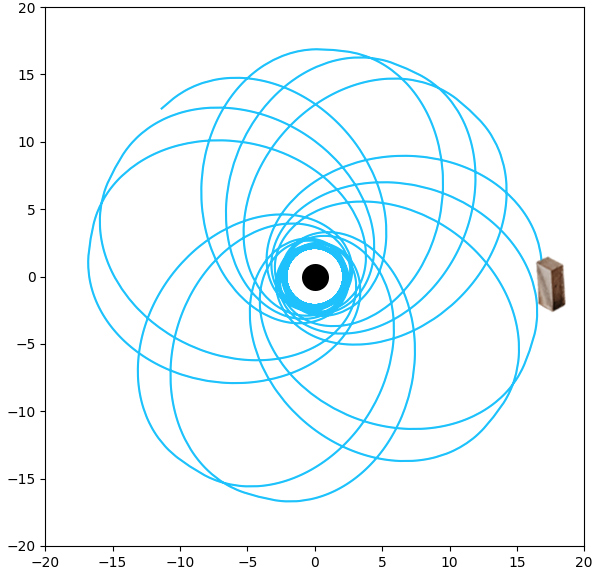
Figuur 124
De grafiek van φ (x, y) voor E = 0.97603696, J = 1.9, Rs = 1,
10 × 5 = 50 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 125
De grafiek van φ (x, y) voor E = 0.9704, J = 1.888, Rs = 1,
2 rondjes om het zwarte gat,
1.999.997 intervallen

Figuur 126
De grafiek van φ (x, y) voor E = 0.9704, J = 1.888, Rs = 1,
10 × 2 = 20 rondjes om het zwarte gat,
19.999.979 intervallen

Figuur 127
De grafiek van φ (x, y) voor E = 0.9704, J = 1.888, Rs = 1,
50 × 2 = 100 rondjes om het zwarte gat,
99.999.899 intervallen

Figuur 128
De grafiek van E (J) met daarin de punten (de groene bolletjes)
van de voorgaande figuren,
D > 0, E < 1, u < n2, Rs = 1
Belangrijke vergelijkingen
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting
De Schwarzschild-oplossing:
































Samenvatting
- Afleidingen van de vergelijkingen
- Onderzoek van de functie
- De effectieve potentiaal
- Nulpunten in de noemer
- Radiële inval
- Invallende banen vanaf ‘ver weg’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D < 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' < 0)
- Stabiele banen vanaf ‘ver weg’ en ‘dichtbij’ (D = 0)
- Invallende banen vanaf ‘dichtbij’ (D = 0, q'' > 0)
- Invallende banen vanaf ‘dichtbij’ (D > 0)
- Stabiele open banen (D > 0)
- Stabiele gesloten banen (D > 0)
- Belangrijke vergelijkingen
- Samenvatting

- D < 0: één nulpunt.
- D = 0: twee nulpunten,
- D > 0: drie nulpunten,
 D < 0 |
 D = 0 |
 D > 0 |
| Tabel 2 | ||



Figuur 9
De grafiek van E (J),
D = 0, Rs = 1

Figuur 10
De grafiek van J (E),
D = 0, Rs = 1


Figuur 13
De grafiek van V (r) voor J = 0.0 (de rode lijn),
J = 0.5 (de lichtgroene lijn), J = 1.0 (de oranje lijn),
J = 1.5 (de paarse lijn), J = √3 (de blauwe lijn),
J = 2.0 (de grijze lijn), J = 2.5 (de bruine lijn),
J = 3.0 (de lichtbruine lijn), J = 3.5 (de donkergroene lijn),
J = 4.0 (de gele lijn) en J = 4.5 (de lichtblauwe lijn),
Rs = 1




Figuur 129
De grafiek van V (r) voor J = 0.0 (de rode lijn),
J = 0.5 (de lichtgroene lijn), J = 1.0 (de oranje lijn),
J = 1.5 (de paarse lijn), J = √3 (de blauwe lijn),
J = 2.0 (de grijze lijn), J = 2.5 (de bruine lijn),
J = 3.0 (de lichtbruine lijn), J = 3.5 (de donkergroene lijn),
J = 4.0 (de gele lijn) en J = 4.5 (de lichtblauwe lijn),
de roze lijn wordt gevormd door de extrema volgens vergelijking (83),
Rs = 1

Hoe werkt dit uit in de praktijk? Voor D < 0 en E ≥ 1 komt de baksteen van ver weg en verdwijnt onherroepelijk in het zwarte gat, zie het rode gebied in onderstaande figuur (zie hoofdstuk 6 voor alle details).

Figuur 130
De grafiek van E (J) (de blauwe lijn),
D = 0, Rs = 1

Figuur 131
De grafiek van E (J) (de blauwe lijn),
D = 0, Rs = 1

Figuur 78
(= figuur 64 (de blauwe lijn) + figuur 71 (de rode lijn))
De grafiek van φ (x, y) voor J = 4, E = 1.6491982708836967,
D = 0, n1 = −0.268, n2/3 = 0.634, 1/n2/3 = 1.578, q'' = 2.713 ∙ 10−2, Rs = 1,
427.365.628 datapunten

Figuur 132
De grafiek van E (J) (de blauwe lijn),
D = 0, Rs = 1

Figuur 133
De grafiek van φ (x, y) voor E = 2.01177, J = 5, Rs = 1,
2 rondjes om het zwarte gat,
1.999.997 intervallen

Figuur 134
De grafiek van E (J) (de blauwe lijn),
D = 0, Rs = 1

Figuur 135
De grafiek van E (J) (de blauwe lijn),
D = 0, Rs = 1

Figuur 110
De grafiek van φ (x, y) voor E = 0.996, J = 5, Rs = 1,
10 rondjes om het zwarte gat,
19.999.979 intervallen
| Condities | Baan van de baksteen | |||
| J = 0 | De baksteen valt radieel in het
zwarte gat (0 < u < 1/Rs oftewel Rs < r < ∞)   |
|||
| D < 0 | E ≥ 1 | De baksteen eindigt in het
zwarte gat vanaf ‘ver weg’ (0 < u < 1/Rs oftewel Rs < r < ∞)    |
||
| E < 1 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n1 < u < 1/Rs oftewel Rs < r < 1/n1)    |
|||
| D = 0 | q'' < 0 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n1 < u < 1/Rs oftewel Rs < r < 1/n1)    |
||
| q'' > 0 | E ≥ 1 | u > n2/3 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n2/3 < u < 1/Rs oftewel Rs < r < 1/n2/3)    |
|
| u < n2/3 | De baksteen eindigt in een baan om het
zwarte gat vanaf ‘dichtbij’ (n1 < u < n2/3 oftewel 1/n2/3 < r < 1/n1)    |
|||
| E < 1 | De baksteen eindigt in een baan om het
zwarte gat vanaf ‘ver weg’ (0 < u < n2/3 oftewel 1/n2/3 < r < ∞)    |
|||
| D > 0 | u > n3 | De baksteen eindigt in het
zwarte gat vanaf ‘dichtbij’ (n3 < u < 1/Rs oftewel Rs < r < 1/n3)    |
||
| u < n2 | E ≥ 1 | De baksteen beweegt in een stabiele open baan om het
zwarte gat (0 < u < n2 oftewel 1/n2 < r < ∞)    |
||
| E < 1 | De baksteen beweegt in een stabiele gesloten baan om het
zwarte gat (n1 < u < n2 oftewel 1/n2 < r < 1/n1)    |
|||
| Tabel 8 | ||||






 Door naar het volgende vraagstuk: de snelheid van een baksteen die in een zwart gat valt
Door naar het volgende vraagstuk: de snelheid van een baksteen die in een zwart gat valt Terug naar het vorige vraagstuk: de invaltijd van een baksteen die in een zwart gat valt
Terug naar het vorige vraagstuk: de invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 10
Vectoren, vraagstuk 10 Vectoren, vraagstuk 48
Vectoren, vraagstuk 48 Vectoren, vraagstuk 86
Vectoren, vraagstuk 86 Wat is de metrische tensor?
Wat is de metrische tensor? De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van Het getal pi
Het getal pi Uitleg artikel algemene relativiteitstheorie: paragraaf 8
Uitleg artikel algemene relativiteitstheorie: paragraaf 8 Het Doppler-effect
Het Doppler-effect De ART-vergelijkingen in componenten van de metrische tensor
De ART-vergelijkingen in componenten van de metrische tensor Het traagheidsmoment van een homogene ronde ster
Het traagheidsmoment van een homogene ronde ster Klassieke afleiding van de formule van Heaviside
Klassieke afleiding van de formule van Heaviside De illusies die wij leven
De illusies die wij leven De illusie van economische groei
De illusie van economische groei Bevrijd uw kind!
Bevrijd uw kind! Waarom Homo Sapiens?
Waarom Homo Sapiens? Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2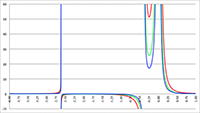 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen