De uitdijing van het heelal
Het heelal dijt uit.
Dat leiden we af uit het feit dat (nagenoeg) alles in het universum zich van ons verwijdert, maar dat is toch raar?
Of heel toevallig?
En iemand ‘ergens verderop’ in het heelal ziet dan toch van alles op zich afkomen?
Om te illustreren dat de uitdijing van het heelal onafhankelijk is van de plek van de waarnemer beschouw ik een heel
lang elastiek.
Ik heb slechts een deel van het elastiek getekend, want stel je maar voor dat het elastiek zich nog heel ver naar beide
kanten uitstrekt.
Voor de duidelijkheid breng ik maatstreepjes aan op het elastiek, bijvoorbeeld na iedere meter één.
Ergens op het elastiek bevindt zich een kabouter met een rood mutsje.
Vervolgens rek ik het elastiek een stuk uit en het uitgerekte elastiek teken ik er voor de duidelijkheid onder.
Door het uitrekken verschuiven de maatstreepjes en ik zorg dat het maatstreepje waar de kabouter staat op dezelfde plaats
blijft, want de kabouter blijft ondanks het uitrekken natuurlijk op hetzelfde maatstreepje staan (ik rek het elastiek dus
niet zo wild uit dat de kabouter omvalt).
De kabouter ziet dat alle maatstreepjes zich van hem verwijderen en hij ziet ook dat de maatstreepjes die verder van hem weg
staan zich meer van hem verwijderen dan de dichterbij gelegen maatstreepjes.
Ergens anders op het elastiek staat nog een kabouter, hij heeft een geel mutsje.
Hoe ervaart hij het uitrekken van het elastiek?
Daarvoor moet ik eerst de tekening van het onderste elastiek een stukje verschuiven zodat ‘zijn’ maatstreepje (het maatstreepje
waar hij zich bevindt) zich na het uitrekken van het elastiek nog steeds op zijn positie bevindt (ik rek het elastiek immers
niet zo wild uit dat de kabouters omvallen).
Nu zijn de maatstreepjes uitgelijnd zodat het maatstreepje waar de kabouter met het gele mutsje staat voor en na het uitrekken
niet verschoven is.
De kabouter met het gele mutsje ziet ook dat alle maatstreepjes zich van hem verwijderen en hij ziet ook dat de maatstreepjes
die verder van hem weg staan zich meer van hem verwijderen dan de dichterbij gelegen maatstreepjes.
Er bevindt zich nog een derde kabouter op het elastiek, deze heeft een blauw mutsje.
Om zijn kijk op het hele gebeuren, het uitrekken van het elastiek, duidelijk te maken moet ik weer dezelfde procedure volgen,
dus ik lijn de tekening van het onderste elastiek zo uit dat ‘zijn’ maatstreepje (het maatstreepje waar hij zich bevindt)
zich na het uitrekken van het elastiek nog steeds op zijn positie bevindt.
Ook de kabouter met het blauwe mutsje ziet dat alle maatstreepjes zich van hem verwijderen en hij ziet ook dat de maatstreepjes
die verder van hem weg staan zich meer van hem verwijderen dan de dichterbij gelegen maatstreepjes.
Alle kabouters zien dus op exact dezelfde manier het maatstreepjespatroon veranderen.
In het volgende plaatje probeer ik dat te laten zien door alles samen te nemen (maar daardoor ziet het plaatje er wel wat
chaotisch uit).
Hoeveel kabouters er ook op het elastiek staan, ze zullen allemaal de uitrekking van het elastiek op precies dezelfde wijze
waarnemen.
Dit alles brengt ons bij de volgende conclusies:
 |
iedere kabouter ziet dat alle maatstreepjes zich van hem verwijderen, |
 |
iedere kabouter ziet de maatstreepjes om hem heen zich op dezelfde manier verwijderen, volgens hetzelfde patroon, |
 |
iedere kabouter ziet de verwijdering van de maatstreepjes toenemen met de afstand, sterker nog,
hij ziet de verwijdering van de maatstreepjes evenredig toenemen met de afstand, |
 |
iedere kabouter ziet de verwijderingssnelheid van de maatstreepjes toenemen met de afstand, en ook hier geldt dat
hij de verwijderingssnelheid evenredig ziet toenemen met de afstand, |
 |
iedere kabouter zou kunnen denken dat hij zich op het midden van het elastiek bevindt. |
Wanneer je in dit hele verhaal het elastiek vervangt door het heelal dan blijven de bovenstaande vijf conclusies
onverminderd geldig.
De vierde conclusie staat nu in de boeken als de wet van Hubble en de evenredigheidsconstante tussen de
verwijderingssnelheid van een object en de afstand tot dat object is de constante van Hubble H0.
Deze constante (die helemaal niet constant is, maar varieert met de tijd) bedraagt ongeveer zeventig kilometer per seconde
per megaparsec, of in gewone mensentaal: dit betekent dat er iedere seconde per 441.000.000.000.000.000 meter universum
één meter universum bijkomt.
Op kleine schaal, naar kosmische begrippen dan, merken we daar helemaal niets van.
De afstand van de Aarde tot de Zon, 150.000.000.000 meter, neemt als gevolg van de uitdijing van het heelal per seconde
minder dan een miljoenste meter toe en dat is niet alleen volkomen onmeetbaar, maar valt ook in het niet bij alle andere
krachten die binnen ons zonnestelsel actief zijn.

De Melkweg en Andromeda liggen op ramkoers en
gaan in een verre toekomst met elkaar botsen om
vervolgens één groot sterrenstelsel te vormen,
dit is een impressie daarvan
Pas op wat grotere schaal begint de uitdijingssnelheid van het heelal een factor van belang te worden.
Het sterrenstelsel Andromeda is de grote zus van de Melkweg en staat op een afstand van 23.650.000.000.000.000.000.000 meter.
Andromeda ligt op ramkoers met de Melkweg, want beide stelsels vliegen met een snelheid van 110 kilometer per seconde op
elkaar af.
Wanneer ik 23.650.000.000.000.000.000.000 deel door 441.000.000.000.000.000 dan levert dat ruim vijftig kilometer per seconde op.
Zonder uitdijing van het heelal zou Andromeda dus met 110 + 50 = 160 kilometer per seconde op ons afstormen, hetgeen impliceert
dat de heelaluitdijing ons minstens een miljard jaar extra respijt geeft voor de grote botsing plaatsvindt.




















 Door naar het volgende vraagstuk: de snelheid van een baksteen die in een zwart gat valt
Door naar het volgende vraagstuk: de snelheid van een baksteen die in een zwart gat valt Terug naar het vorige vraagstuk: ruimtetijdkromming
Terug naar het vorige vraagstuk: ruimtetijdkromming Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 70
Vectoren, vraagstuk 70 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van Boeken die uitsteken
Boeken die uitsteken Relativiteitstheorie rekenkundig, hoofdstuk 6: voelen
Relativiteitstheorie rekenkundig, hoofdstuk 6: voelen De relativistische rotatie-energie van een holle bol
De relativistische rotatie-energie van een holle bol Voorbeelden van E = mc2
Voorbeelden van E = mc2 Elektriciteit en magnetisme
Elektriciteit en magnetisme De grote vragen in het leven
De grote vragen in het leven De illusie van de grote gevaren
De illusie van de grote gevaren De reis naar de werkelijkheid van Anita Moorjani
De reis naar de werkelijkheid van Anita Moorjani Volgen, achtervolgen, vervolgen en de gevolgen
Volgen, achtervolgen, vervolgen en de gevolgen Tranen
Tranen De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat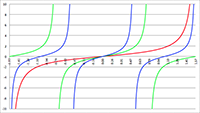 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)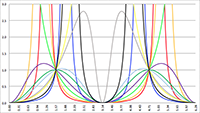 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2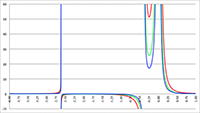 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen