De relativistische bewegingsvergelijkingen
Bereken de relativistische effecten op de bewegingsparameters (afstand, snelheid, versnelling en tijd) in het
geval van niet-constante snelheden (versnellingen) en maak daarbij alleen gebruik van formules uit de
speciale relativiteitstheorie.
Ga ervan uit dat er geen (significante) massa’s in de buurt zijn.
Binnen de speciale relativiteitstheorie werken we met constante snelheden.
Het is natuurlijk ook wel leuk (toch?) om dat andere gebied te verkennen waar snelheden van moment tot moment
kunnen veranderen.
En wanneer snelheden veranderen zijn er versnellingen aan het werk (of vertragingen, maar dat zijn negatieve
versnellingen).
De uitdaging is om daar aan te rekenen met de simpele formules van de speciale relativiteitstheorie en niet
gelijk het zware wiskundige apparaat van de
algemene relativiteitstheorie uit de kast te hoeven halen.
Zolang snelheden constant zijn is het leven heerlijk simpel, want rekenen met ‘iets’ dat van moment tot moment
gelijk blijft is veel eenvoudiger dan rekenen met ‘iets’ dat continu aan verandering onderhevig is.
De afgelegde weg is de
integraal
van de snelheid en versnelling is de
afgeleide van de snelheid en dat
rekent heel gemakkelijk wanneer de snelheid constant is.
Voor twee waarnemers, W
1 en W
2, die met een snelheid v ten opzichte van elkaar bewegen
is onderstaande tabel dan snel ingevuld:
|
W1 |
W2 |
| Afgelegde weg |
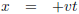 |
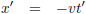 |
| Snelheid |
 |
 |
| Versnelling |
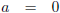 |
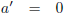 |
| Tabel 1: bewegingsparameters bij constante snelheid |
Vervolgens is het een kwestie van de
Lorentz-transformaties ter hand nemen om de waarnemingen
van W1 en W2 in elkaar om te kunnen rekenen.
Versnelling is gedefinieerd als snelheidsverandering per verstreken tijd.
Maar hoe ziet versnelling eruit relativistisch gezien?
Een waarnemer W1 ziet een tweede waarnemer, W2, voorbijkomen met een constante snelheid +v.
Waarnemer W2 ziet W1 daarom met een snelheid −v.
Op een bepaald moment, t0 voor W1, t0' voor W2, zet W2 een
constante versnelling a0' in gang.
Na een heel klein tijdje dt' is zijn snelheid een heel klein beetje dv' toegenomen:
W
1 zag eerst W
2 met een snelheid v en nu ziet hij hem met een iets hogere snelheid v + dv.
W
1 neemt een snelheidsverandering waar van dv en voor W
2 is dat dv'.
Vervolgens komt W
2 op het idee om de twee snelheden, zoals waargenomen door W
1,
relativistisch van elkaar af te trekken om zodoende een relatie te vinden tussen dv' en dv.
Want vanuit W
2 gezien moet het verschil dv, zoals waargenomen door W
1, via een
relativistische vertaalslag overeenkomen met zijn dv'.
Het
relativistisch optellen van snelheden
(of aftrekken, want dat is het optellen van een negatieve snelheid) gaat als volgt:
En daar maken we nu gebruik van:
Omdat dv
infinitesimaal klein is
en daarom te verwaarlozen is ten opzichte van v gaat deze vergelijking over in (hierin is γ de
Lorentz-factor):
Oftewel, na combinatie met vergelijking (1):
De volgende stap is dat we beide zijden van vergelijking (5) gaan
integreren:
Omdat de versnelling a
0' constant is haal ik die buiten de
integraal:
Ik heb hier gebruik gemaakt van de
tabel met integralen.
En om het geheugen even op te frissen, dit is de
tangens hyperbolicus:
En de functie artanh is de inverse functie van de
tangens hyperbolicus,
de
area tangens hyperbolicus.
Voor het gemak kies ik mijn beginwaarden zo dat:
Waardoor ik van vergelijking (7) dit overhoud:
Ik heb hier t' staan als functie van v, maar het omgekeerde is natuurlijk veel interessanter.
Na heel weinig geknutsel heb ik dit:
De breuk a
0't'/c gaan we nog veel vaker tegenkomen en daarom stel ik:
Waardoor (11) overgaat in:
Oftewel:
Waar W
1 en W
2 het over eens zijn is hun relatieve snelheid, want die moet voor beide
waarnemers overeenkomen.
Daarom kan ik voor vergelijking (13a) ook schrijven:
Ik ga gebruik maken van de reeksontwikkeling van de
e-macht.
In de tabel met Taylor-reeksen vinden we:
Merk op dat voor lage waarden van t', dus wanneer het versnellen net is begonnen en de snelheid nog laag is,
we het volgende kunnen schrijven voor de
tangens hyperbolicus:
Daardoor gaat vergelijking (13) over in de klassieke formule:
Gaat t' daarentegen naar oneindig dan gaat de
tangens hyperbolicus naar één:
Waardoor vergelijking (13) wordt:
In het limietgeval nadert de snelheid v naar c (maar die zal nimmer bereikt worden).
De volgende twee stappen zijn relatief simpel want de afgelegde weg is de
integraal van de snelheid en versnelling
is de
afgeleide van de snelheid.
Ik bereken eerst de afgelegde weg:
Ik heb hier weer gebruik gemaakt van de
tabel met integralen.
Met behulp van vergelijking (13b) kan ik dit ook schrijven als:
De
cosinus hyperbolicus is te schrijven als een
functie van de tangens hyperbolicus:
Nu ga ik gebruik maken van de
reeksontwikkeling van de
natuurlijke logaritme.
In de
tabel met Taylor-reeksen vinden we:
Ik onderzoek weer even de limietgevallen, eerst voor t' nadert naar nul.
De
logaritme van de
cosinus hyperbolicus wordt dan:
Vergelijking (19) wordt dan:
Hetgeen inderdaad weer is wat we klassiek zouden verwachten.
En indien t' naar oneindig gaat dan ontstaat:
Dan wordt vergelijking (19):
En dit is helemaal in overeenstemming met onze relativistische verwachtingen.
Tenslotte bereken ik nog de versnelling (met behulp van vergelijking (13)):
Dit kan ik wederom ook anders opschrijven.
De
secans hyperbolicus is te schrijven als een
functie van de tangens hyperbolicus
en ik maak gebruik van vergelijking (13a):
Ik onderzoek weer even de limietgevallen, eerst voor t' nadert naar nul.
De
cosinus hyperbolicus
wordt dan:
Waarmee vergelijking (25) wordt:
Hetgeen inderdaad weer is wat we klassiek zouden verwachten.
En indien t' naar oneindig gaat dan ontstaat:
Dan wordt vergelijking (25):

Moeder Natuur
En dit is weer helemaal in overeenstemming met onze relativistische verwachtingen.
Voor t' = ∞ versnellen ze simpelweg niet meer, wat ze ook doen.
Ergens ligt een grens, omdat de lichtsnelheid niet kan worden overschreden.
Moeder Natuur zegt hier “het is mooi geweest!”.
Zo komen we tot het volgende overzicht:
|
W2 |
Limiet voor t’ → 0 |
Limiet voor t’ → ∞ |
| Afgelegde weg |
 |
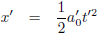 |
 |
| Snelheid |
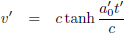 |
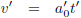 |
 |
| Versnelling |
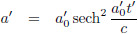 |
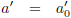 |
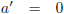 |
| Tabel 2: bewegingsparameters bij constante versnelling voor W2 |

De grafiek van x’ als functie van t’ voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)

De grafiek van v’ als functie van t’ voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)

De grafiek van a’ als functie van t’ voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)
Verder hebben we natuurlijk ook nog de formule voor
tijddilatatie tot onze beschikking,
waargenomen vanuit W
1:
Uit de vergelijkingen (5) en (30) volgt:
Nu hebben we alles wat we willen weten naar het referentiestelsel van W
1 vertaald.
De volgende stap is weer dat we beide zijden van deze vergelijking gaan
integreren:
Hier heb ik nogmaals gebruik gemaakt van de
tabel met integralen.
Ik kies mijn beginwaarden weer comfortabel:
Waardoor ik dit overhoud:
Ik heb hier t staan als functie van v, maar ik ga weer naar het omgekeerde toewerken:
Ik onderzoek weer even de limietgevallen, eerst voor t nadert naar nul en daarna voor t gaat naar oneindig:
Wederom geen verrassingen.
De volgende twee stappen zijn weer het uitrekenen van de afgelegde weg en de versnelling.
Ik bereken eerst de afgelegde weg:
Ik heb nogmaals gebruik gemaakt van de
tabel met integralen.
Met behulp van vergelijking (34) kan ik dit ook schrijven als volgt:
En vervolgens onderzoek ik weer de limietgevallen, eerst voor t nadert naar nul en daarna voor t gaat naar oneindig:
Ook deze resultaten zijn helemaal volgens verwachting.
Tenslotte bereken ik nog de versnelling:
Merk op dat ik ook vergelijking (31) had kunnen nemen om het volgende te doen:
Op deze manier vind ik een vergelijking om de
momentane versnelling om te rekenen naar het andere stelsel
als functie van de
momentane snelheid.
Dat is echter niet wat we zoeken, we willen uitdrukkingen als functie van de tijd.
Ik onderzoek voor de laatste maal de limietgevallen, eerst voor t nadert naar nul en daarna voor t gaat naar oneindig:
En ook deze laatste resultaten zijn wat we verwacht hadden.
Zo komen we tot het volgende overzicht:
|
W1 |
Limiet voor t → 0 |
Limiet voor t → ∞ |
| Afgelegde weg |
 |
 |
 |
| Snelheid |
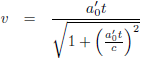 |
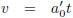 |
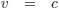 |
| Versnelling |
 |
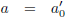 |
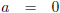 |
| Tabel 3: bewegingsparameters bij constante versnelling voor W1 |
Om goed te kunnen vergelijken zet ik tabel twee er nogmaals bij:
|
W2 |
Limiet voor t’ → 0 |
Limiet voor t’ → ∞ |
| Afgelegde weg |
 |
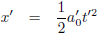 |
 |
| Snelheid |
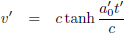 |
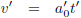 |
 |
| Versnelling |
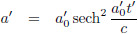 |
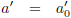 |
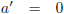 |
| Tabel 2: bewegingsparameters bij constante versnelling voor W2 |
Ondanks dat we hele verschillende uitdrukkingen gevonden hebben voor de beide waarnemers voor afstand,
snelheid en versnelling komen in de limietgevallen de waarnemingen exact overeen.
Voor t = 0 gaan bij beide waarnemers de bewegingsvergelijkingen over in die van de klassieke mechanica
en wanneer t naar oneindig gaat lopen ze tegen dezelfde relativistische beperkingen aan.

De grafiek van x als functie van t voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)

De grafiek van v als functie van t voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)

De grafiek van a als functie van t voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)
Nu ontbreekt er nog één belangrijk ding, namelijk het omrekenen van de tijd in het ene referentiestelsel
naar de tijd in het andere referentiestelsel.
Zoals gezegd, waar W
1 en W
2 het over eens zijn is hun relatieve snelheid, want die
moet voor beide waarnemers overeenkomen (de vergelijkingen (11) en (35)):
Hiermee kunnen we de afgelegde weg als functie van de tijd, x (t) = vergelijking (38), ook schrijven als functie van t'
(dat is wel handig om bij de hand te hebben):
En het resultaat van vergelijking (44) is rechtstreeks omkeerbaar tot:
En wat zijn dan de limietgevallen van de beide tijden?
Dat ga ik ook nog even uitzoeken, eerst voor de extrema van t':
Voordat ik de volgende limieten ga uitrekenen wil ik er nog even op wijzen dat je de
area sinus hyperbolicus
kunt
omschrijven naar een
natuurlijke logaritme,
en vice versa, als volgt:
In de
tabel met Taylor-reeksen vinden we:
Nu komen de extrema van t:
Voor lage waarden van t lopen beide tijden nog synchroon, maar dat wordt uiteindelijk heel anders.
De tijden gaan dan exponentieel respectievelijk
logaritmisch uit de pas lopen!
Na al dit gereken is ons overzicht compleet:
|
W1 |
W2 |
| Afgelegde weg |
 |
 |
| Snelheid |
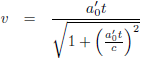 |
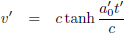 |
| Versnelling |
 |
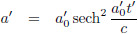 |
| Tijd |
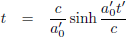 |
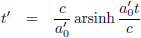 |
| Tabel 4: bewegingsparameters bij constante versnelling |
Hier wordt het grote verschil met constante snelheden zichtbaar.
De
tijddilatatie bij constante snelheid is
gezien vanuit de ene waarnemer, respectievelijk de andere waarnemer:
Hier hebben we te maken met een volkomen symmetrische situatie.
De
tijddilatatie bij constante versnelling is echter:
Wanneer er versnelling in het spel komt dan is de situatie
niet meer symmetrisch!

De grafiek van t als functie van t’ voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)

De grafiek van t’ als functie van t voor a
0’ = 10 m/s
2,
klassiek (de rode lijn) en relativistisch (de groene lijn)
Ik laat nog wat vergelijkende grafieken zien.
Hieronder staan vier grafieken waarbij op de horizontale as een periode van tien miljoen seconden is uitgezet
(ruim 115 dagen).
Tot ongeveer een miljoen seconden (ruim anderhalve week) gaan klassiek en relativistisch gelijk op, maar
geleidelijk worden kleine verschillen zichtbaar.

De grafiek van x’ als functie van t’ (de groene lijn), x als functie van t (de blauwe lijn)
en klassiek (x = 0.5a
0’t
2, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van v’ als functie van t’ (de groene lijn), v als functie van t (de blauwe lijn)
en klassiek (v = a
0’t, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van a’ als functie van t’ (de groene lijn), a als functie van t (de blauwe lijn)
en klassiek (a = a
0’, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van t’ als functie van t (de groene lijn), t als functie van t’ (de blauwe lijn)
en klassiek (t = t’, de rode lijn) voor a
0’ = 10 m/s
2
Hieronder staan vier grafieken waarbij op de horizontale as een periode van een miljard seconden is uitgezet
(ruim dertig jaar).
De relativistische effecten worden overduidelijk zichtbaar.
Niets kan sneller dan het licht en de tijd wordt voor reiziger en achterblijver onverenigbaar.
De rode lijnen zijn volgens de klassieke wetten en deze worden hopeloos onbruikbaar.

De grafiek van x’ als functie van t’ (de groene lijn), x als functie van t (de blauwe lijn)
en klassiek (x = 0.5a
0’t
2, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van v’ als functie van t’ (de groene lijn), v als functie van t (de blauwe lijn)
en klassiek (v = a
0’t, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van a’ als functie van t’ (de groene lijn), a als functie van t (de blauwe lijn)
en klassiek (a = a
0’, de rode lijn) voor a
0’ = 10 m/s
2

De grafiek van t’ als functie van t (de groene lijn), t als functie van t’ (de blauwe lijn)
en klassiek (t = t’, de rode lijn) voor a
0’ = 10 m/s
2
Tenslotte wil ik nog iets onder de aandacht brengen.
Ik ga tabel 4 nogmaals opschrijven, maar dan met β erin:
|
W1 |
W2 |
| Afgelegde weg |
 |
 |
| Snelheid |
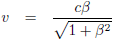 |
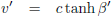 |
| Versnelling |
 |
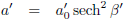 |
| Tijd |
 |
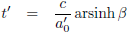 |
| Tabel 5: bewegingsparameters bij constante versnelling als functie van β |
Kijk, dat ziet er al veel mooier uit.
Eerder stelde ik:
Maar ik had ook kunnen stellen:
Dan krijgt tabel 5 deze bijzondere aanblik:
|
W1 |
W2 |
| Afgelegde weg |
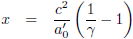 |
 |
| Snelheid |
 |
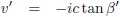 |
| Versnelling |
 |
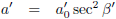 |
| Tijd |
 |
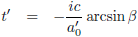 |
| Tabel 6: bewegingsparameters bij constante versnelling met imaginaire β |
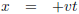
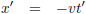


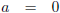
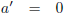




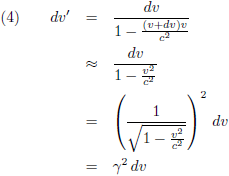
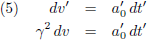
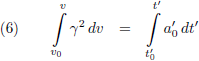

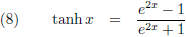
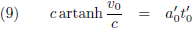
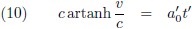
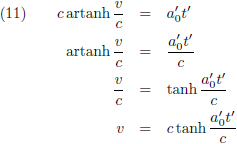
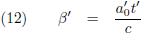

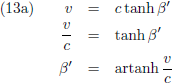

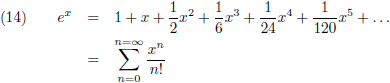
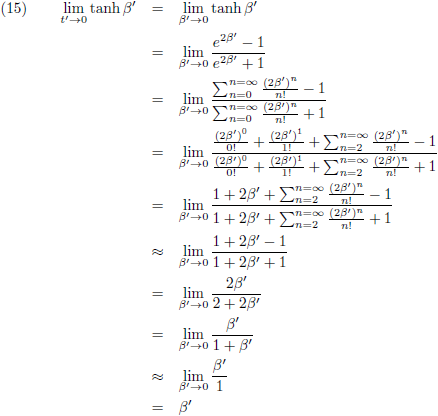


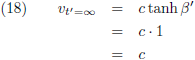
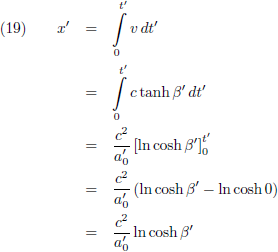
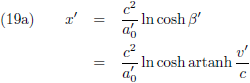



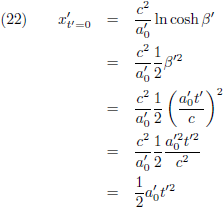
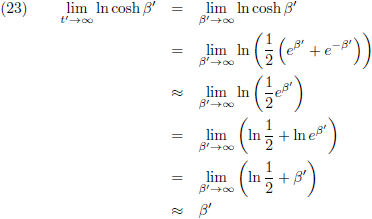


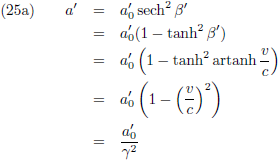
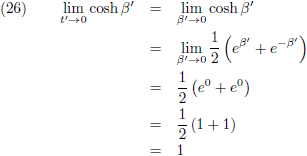

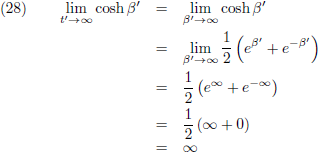
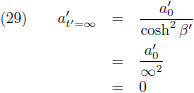


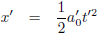

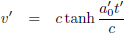
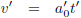

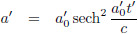
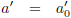
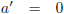




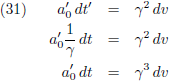
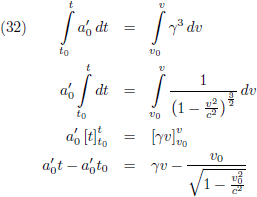

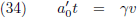


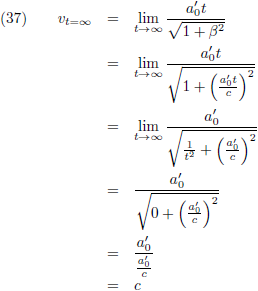


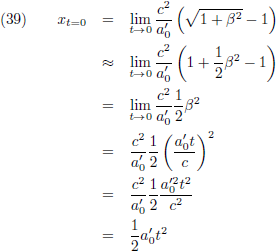

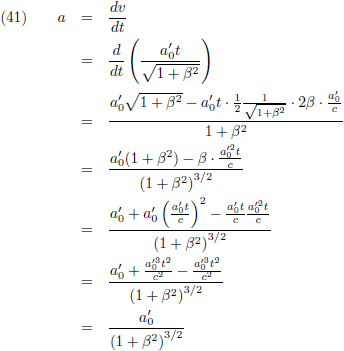
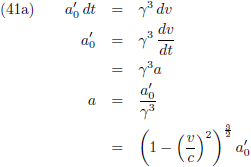
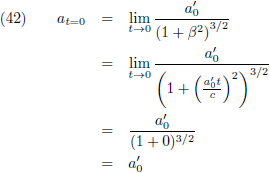
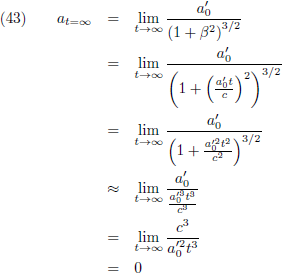



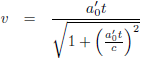
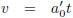
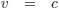

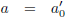
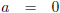

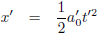

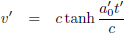
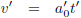

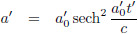
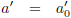
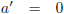




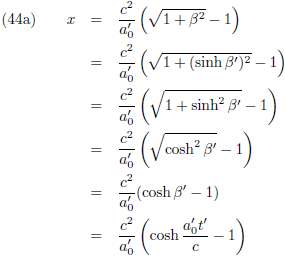
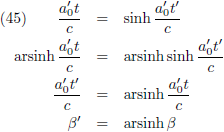

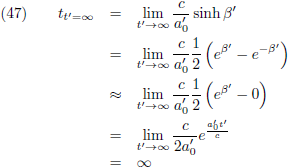
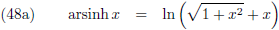
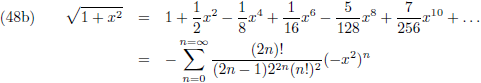
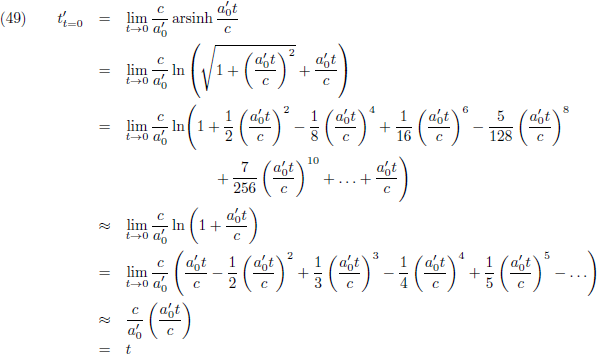
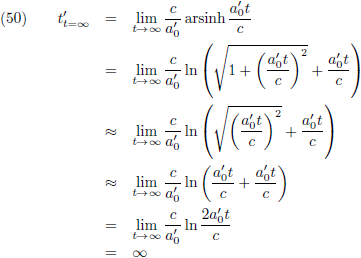


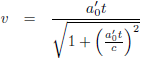
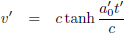

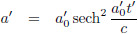
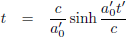
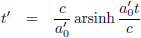
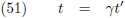

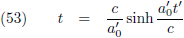
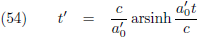












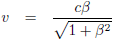
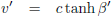

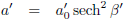

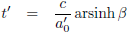
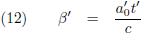
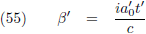
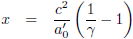


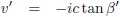

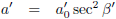

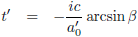


 Door naar het volgende vraagstuk: de SuperLamborghini
Door naar het volgende vraagstuk: de SuperLamborghini Terug naar het vorige vraagstuk: de transformatievergelijking voor de energie van EM-golven
Terug naar het vorige vraagstuk: de transformatievergelijking voor de energie van EM-golven Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie Binnen een mensenleven het heelal doorkruisen
Binnen een mensenleven het heelal doorkruisen Een ruimtereis naar het sterrenstelsel Andromeda
Een ruimtereis naar het sterrenstelsel Andromeda De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 44
Vectoren, vraagstuk 44 Vectoren, vraagstuk 82
Vectoren, vraagstuk 82 Alle symmetrieën van de Riemann-tensor
Alle symmetrieën van de Riemann-tensor De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van Bijzondere figuren
Bijzondere figuren Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk B
Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk B De Lorentz-transformaties
De Lorentz-transformaties Lineariteit van de Lorentz-transformaties
Lineariteit van de Lorentz-transformaties De stabiliteit van de Lagrange-punten
De stabiliteit van de Lagrange-punten De wetten van Maxwell met potentialen
De wetten van Maxwell met potentialen De illusies die wij leven
De illusies die wij leven De illusie dat ik moet weten wat er in de wereld gebeurt
De illusie dat ik moet weten wat er in de wereld gebeurt Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat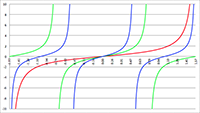 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)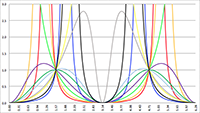 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2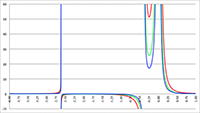 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen