De contourintegraal van
f (x) = 1/(a2 + x2)
Trefwoorden/keywords: contourintegraal/contourintegral, integreren/integrate, f (x) = 1/(a2 + x2)

De grafiek van f (x) = 1/(a
2 + x
2) voor a = 1 (de rode lijn),
a = 2 (de groene lijn) en a = 3 (de blauwe lijn)
Deze
integraal ga ik oplossen als
contourintegraal.
Zoals gebruikelijk begin ik door mijn probleem over te hevelen naar het
complexe vlak en dat doe ik door
simpelweg iedere x in het functievoorschrift te vervangen door een z:
Ik ga een plaatje maken van f (z) en daarom ga ik de functie eerst anders opschrijven:

De grafiek van f (z) = 1/(a
2 + z
2) voor a = 1
Ik maak de grafiek nog een keer, maar dan met
eenheidsvectoren, dat ziet er wat duidelijker uit.

De grafiek van f (z) = 1/(a
2 + z
2) (genormaliseerd) voor a = 1
Ik zoek de functie op in de
holomorfietabel van complexe functies
en ik vind dat de functie overal
holomorf is (elders op
het internet wordt hier altijd blind van uitgegaan, maar dat moet toch echt wel even gecheckt worden), behalve
voor z = p
1 en z = p
2 (de beide
polen,
daar waar de noemer van de functie nul wordt):
Er zijn dus twee
polen
en die teken ik erbij in de grafiek.
Voor a = 1 bevinden de
polen
zich op +i en −i.

De grafiek van f (z) = 1/(a
2 + z
2) (genormaliseerd) voor a = 1
en de beide
polen (de blauwe stippen)
Vervolgens ga ik een
contour aanleggen en een onderdeel
daarvan moet zijn van x = −∞ tot x = +∞, want dat is immers de probleemstelling waar ik mee begon.

De grafiek van f (z) = 1/(a
2 + z
2) (genormaliseerd) voor a = 1,
de beide
polen (de blauwe stippen)
en het
contour van x = −∞ tot x = +∞
(de rode lijn)
Nu moet ik het
contour nog wel sluiten (want om
redenen die weldra duidelijk worden wil ik graag een
gesloten contour) en dat doe ik met een
halve cirkel die de beide uiteinden van het
contour
van x = +∞ tot x = −∞ met elkaar verbindt.

De grafiek van f (z) = 1/(a
2 + z
2) (genormaliseerd) voor a = 1,
de beide
polen (de blauwe stippen)
en het
gesloten contour (de rode lijn)
De
contourintegraal is de som van de
integralen over alle
deel
contouren:
Volgens de Cauchy-residustelling
geldt:
Waarbij voor het residu geldt:
Hiermee wordt het linkerlid van de
contourintegraal:
De eerste term van het rechterlid is mijn oorspronkelijke probleem (want voor dat deel van het
contour is het
imaginaire deel nul en geldt dus dat z = x):
Dan rest mij nog om de laatste term aan te pakken:
Omdat z over het hele
contour γ
2
oneindig is mag ik schrijven:
Voor z kan ik schrijven (met r een oneindige constante, en φ varieert van 0 tot π):
Hiermee wordt de vorige vergelijking:
De bijdrage aan de
integraal van het
contour γ
2 is dus nul.
Ik vond voor de beide
polen:
De
pool p
1 wordt omsloten door het
contour en daarom ga ik die
pool buiten de functie brengen:
Waaruit volgt:
Hetgeen mij bij het eindantwoord brengt:
In het functievoorschrift is te zien dat het niet uitmaakt of a positief of negatief is, maar in het antwoord
dat ik zojuist gevonden heb is dat niet het geval.
Omdat de functie overal boven de x-as ligt (zie de grafiek) is het antwoord altijd positief en moet ik dus
de
absolute waarde nemen:































 Naar de volgende integraal: de integraal van
Naar de volgende integraal: de integraal van Naar de vorige integraal: de integraal van
Naar de vorige integraal: de integraal van Tabel met integralen
Tabel met integralen Tabel met afgeleiden
Tabel met afgeleiden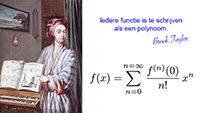 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen Differentiëren
Differentiëren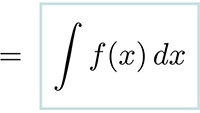 Integreren
Integreren De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van De integralen van
De integralen van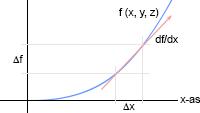 Vectoren, vraagstuk 26
Vectoren, vraagstuk 26 Vectoren, vraagstuk 71
Vectoren, vraagstuk 71 De covariante metrische tensor naar contravariant en vice versa
De covariante metrische tensor naar contravariant en vice versa De Taylor-reeks van
De Taylor-reeks van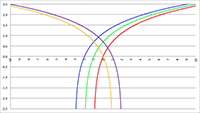 De Taylor-reeksen van
De Taylor-reeksen van Vind de nulpunten van f (x) = ax − xa
Vind de nulpunten van f (x) = ax − xa Holomorfie van de functie
Holomorfie van de functie Integreren van complexe functies
Integreren van complexe functies Uitleg artikel algemene relativiteitstheorie: paragraaf 13
Uitleg artikel algemene relativiteitstheorie: paragraaf 13 Afleiding van de Schwarzschild-oplossing
Afleiding van de Schwarzschild-oplossing De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Taylor-reeksen van
De Taylor-reeksen van De integralen van
De integralen van De integralen van
De integralen van De integralen van
De integralen van De massa van de atmosfeer
De massa van de atmosfeer Hyper-Catalan-getallen
Hyper-Catalan-getallen Een ontmoeting met aliens
Een ontmoeting met aliens Ze durven niet
Ze durven niet Fuss-getallen
Fuss-getallen Ze mogen niet
Ze mogen niet Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen