Afleiding van de Reissner-Nordström-oplossing
Mijn vertrekpunt voor deze afleiding is de Schwarzschild-oplossing:


Volgens de wereldberoemde formule van Einstein zijn energie en massa equivalent:



Dit is de zwaartekrachtwet van Newton:

En dit is de wet van De Coulomb die de elektrische kracht beschrijft:

In de afleiding van de Schwarzschild-oplossing kun je zien dat die via de potentiaalfuncties loopt, en dat de zwaartekracht en de elektrische kracht wiskundig altijd precies de andere kant op gaan blijft je achtervolgen. Er zit altijd een minteken tussen beide! Dit is de reden van het minteken in vergelijking (5).
En vergelijking (5) vul ik in in de Schwarzschild-oplossing. Hierbij wil ik direct opmerken dat ik behoorlijk kort-door-de-bocht te werk ga, want de Schwarzschild-oplossing geldt in een lege (vacuüm) ruimte en dat is uiteraard niet meer het geval wanneer er elektromagnetische velden aanwezig zijn. Dus ik wil niet beweren dat dit een solide afleiding is, maar het geeft wel een goed idee om te laten zien hoe de Reissner-Nordström-oplossing in elkaar steekt. Aldus arriveren we, relatief simpel, bij de Reissner-Nordström-oplossing:


En de metrische tensor ziet er dan zo uit, voor wat we tegenwoordig een zwart gat met elektrische lading noemen:







 Door naar het volgende vraagstuk: een geodetische lijn rondom een puntmassa
Door naar het volgende vraagstuk: een geodetische lijn rondom een puntmassa Terug naar het vorige vraagstuk: het equivalentieprincipe
Terug naar het vorige vraagstuk: het equivalentieprincipe Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie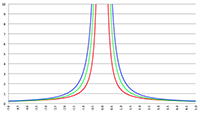 De integraal van
De integraal van De integraal van
De integraal van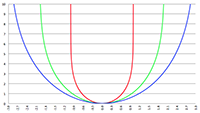 De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van De integralen van
De integralen van Vectoren, vraagstuk 24
Vectoren, vraagstuk 24 Vectoren, vraagstuk 69
Vectoren, vraagstuk 69 Uitschrijven van de sommatieconventie
Uitschrijven van de sommatieconventie De Taylor-reeks van
De Taylor-reeks van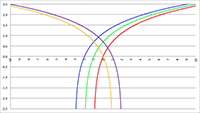 De Taylor-reeksen van
De Taylor-reeksen van Wat is groter?
Wat is groter? Holomorfie van de functie
Holomorfie van de functie Integreren van complexe functies
Integreren van complexe functies Uitleg artikel algemene relativiteitstheorie: paragraaf 11
Uitleg artikel algemene relativiteitstheorie: paragraaf 11 Binnen een mensenleven het heelal doorkruisen
Binnen een mensenleven het heelal doorkruisen De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Kwantummechanica
Kwantummechanica De grote vragen in het leven
De grote vragen in het leven De illusie dat het goed gaat met mij
De illusie dat het goed gaat met mij De Taylor-reeksen van
De Taylor-reeksen van De integralen van
De integralen van De integralen van
De integralen van De integralen van
De integralen van De massa van de atmosfeer
De massa van de atmosfeer Hyper-Catalan-getallen
Hyper-Catalan-getallen Een ontmoeting met aliens
Een ontmoeting met aliens Ze durven niet
Ze durven niet Fuss-getallen
Fuss-getallen Ze mogen niet
Ze mogen niet Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen