Voorbij Einstein | Wiskunde, natuurkunde en filosofie | De Bianchi-identiteit

WETENSCHAPPELIJKE BOEKEN

Home

De integralen van f (x) = tanⁿ (ax)

Ze zijn er niet

De Taylor-reeks van f (x) = 1/(1 − a² cos² x)^1/2

De Taylor-reeks van f (x) = (1 − a² cos² x)^1/2

Samenvatting van de holomorfietabel van complexe functies

1000 doden per minuut

Integreren van complexe functies

Holomorfietabel van complexe functies

Differentiëren van complexe functies

Definities en eigenschappen van complexe getallen

Machten van x neutraliseren middels de gammafunctie

De gammafunctie (functiewaarden)

De gammafunctie

Het explosieve einde van een zwart gat

De verdamptijd van een zwart gat

Een simpele afleiding van de Hawking-straling

Waar begint de spaghettificatie?

De kans op buitenaards leven

De oppervlaktezwaartekracht van een zwart gat

Een simpele afleiding van de Unruh-temperatuur

Wij en buitenaards leven

Voorbeelden van E = mc²

De pijn die je voelt wanneer je in een zwart gat valt

De versnelling van een baksteen die in een zwart gat valt

De snelheid van een baksteen die in een zwart gat valt

De Euler-Lagrange-vergelijking

De baan van een baksteen bij een zwart gat

De Taylor-reeks van f (x) = tan (ax)

De integralen van f (x) = sin² x/(1 + a cos x)²

De integraal van f (x) = 1/(x² (ax² + bx + c))

De invaltijd van een baksteen die in een zwart gat valt

De integraal van f (x) = x^m ln (ax)

De integraal van f (x) = x^p ln (ax)

De versnelling van een baksteen die in een zwart gat valt

De versnelling van een baksteen die in een zwart gat valt

De naam van een zwart gat

De integraal van f (x) = x^p cos (ax)

De integraal van f (x) = x^p sin (ax)

Leid de Boltzmann-verdeling af

De integraal van f (x) = (ax² + bx + c) e^{− (ax² + bx + c)}

De integraal van f (x) = x² e^−ax²

Bereken de energie in een condensator

Bereken de energie in een spoel

De snelheid van een baksteen die in een zwart gat valt

De invaltijd van een baksteen die in een zwart gat valt

Relativiteitstheorie

Kwantummechanica

Elektriciteit en magnetisme

Algemene natuurkunde

Boeken over natuurkunde te koop

De grote vragen in het leven

De illusies die wij leven

Reizigers naar de werkelijkheid

Gedichten over Liefde

Wij en buitenaards leven

Recent toegevoegde pagina’s

Kalender van de jaren 0001 − 3000 met weekdagen

Index: personen

Index: trefwoorden

Notatie en terminologie

Excel bestanden

Fysische gegevens

Woordenboek: Nederlands - Engels

Woordenboek: Engels - Nederlands

Natuurkundeclub β’24

Natuurkundeclub β’24 (openbare pagina)

Natuurkundeclub β’24 (besloten pagina)

Alleen voor leden

Natuurkundeclub β’24

Natuurkundeclub Gℏc

Resumé Watchers

De Bianchi-identiteit

Wat is de Bianchi-identiteit?

Dit is de Riemann-tensor:

Ik ga de Riemann-tensor driemaal opschrijven waarbij de benedenindices telkens een andere positie innemen (of heel netjes gezegd: ik laat ze cyclisch permuteren):

Vervolgens ga ik de vergelijkingen (2a), (2b) en (2c) bij elkaar optellen:

Ik dien nu te bedenken dat de Christoffel-symbolen symmetrisch zijn in de eerste twee indices (de bovenindices):

Met dit in mijn achterhoofd kan ik alle termen in het rechterlid van vergelijking (3) tegen elkaar wegstrepen:

Aldus komen we tot de Bianchi-identiteit:

Dit impliceert dat er een afhankelijkheid zit in de componenten van de Riemann-tensor. En niet eentje, maar een heleboel. In twee dimensies gaat het om 2⁴ = 16 afhankelijke relaties, in drie dimensies zijn het er 3⁴ = 81 en in vier dimensies betreft het maar liefst 4⁴ = 256 relaties. Hebben we daar ook wat aan? Daarover gaat het volgende vraagstuk.

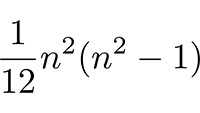Door naar het volgende vraagstuk: onafhankelijke componenten in de Riemann-tensor

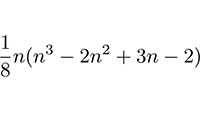Terug naar het vorige vraagstuk: mathematisch verschillende componenten in de Riemann-tensor

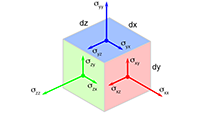Overzichtspagina met vraagstukken

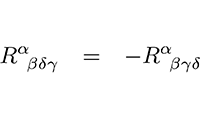Anti-symmetrie in de Riemann-tensor

Alle symmetrieën van de Riemann-tensor

Hoe vormt zich de Ricci-tensor?

Hoe vormt zich de Ricci-scalar?

De integraal van
f (x) = 1/(x³ (a² + x²)^1/2)

De integraal van
f (x) = 1/(1 − cos² (ax))

De integraal van
f (x) = x² ln (a + x)

De integraal van
f (x) = cosⁿ (ax)

De integralen van
f (x) = 1/(1 + a sin x) versus f (x) = 1/(1 + a sin² x)

Vectoren, vraagstuk 18

Vectoren, vraagstuk 56

Vectoren, vraagstuk 94

Tabel met Taylor-reeksen

De Taylor-reeks van
f (x) = 1/(1 − x)^1/2

De stelling van Gauss

Definities en eigenschappen van complexe getallen

Holomorfie van de functie
f (z) = (1 + i) (x + y)²

Relativiteitstheorie rekenkundig

Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie

Stabiliteit van cirkelvormige banen om een centrale massa

De versnelling van een baksteen die in een zwart gat valt

De integralen van f (x) = tanⁿ (ax)

Ze zijn er niet

De Taylor-reeks van f (x) = 1/(1 − a² cos² x)^1/2

De Taylor-reeks van f (x) = (1 − a² cos² x)^1/2

Samenvatting van de holomorfietabel van complexe functies

1000 doden per minuut

Integreren van complexe functies

Overzichtspagina wiskunde

Overzichtspagina natuurkunde

Overzichtspagina filosofie

Doneer enkele euro’s

Wetenschappelijke boeken te koop

Alle rechten voorbehouden / All rights reserved © Karel de Vlieger 2010 − 2024